1. Introduction

In discussing the functionality of a programming language, it is useful to determine whether the computational power of the language is equivalent to general purpose languages such as C, Lisp, and Java; or if its application is necessarily limited to special purposes, as are such languages as Microsoft Excel^® and SQL [Kiper et al 1997]. This determination can be made by demonstrating whether or not a language is Turing complete. Turing completeness implies that any computation that can be performed in the language can be performed on a Turing machine and vice versa. According to the Turing Thesis, any problem that is computable by any machine can be solved using a Turing machine [Linz 1996]. Thus, to show that a language is Turing complete, it is necessary to show only that the language has no less computational power than a Turing machine.

Although commercial spreadsheet languages are not Turing complete, it is possible for a language using the spreadsheet programming paradigm to be Turing complete. One example is the spreadsheet-based visual programming language (VPL) Forms/3. This paper demonstrates Forms/3's Turing completeness with the following implementation of a Turing machine simulator.

2. A Brief Introduction to Programming in Forms/3

As mentioned, programming in Forms/3 follows the spreadsheet paradigm, in that the programmer creates cells on a form, and then enters formulas into each of these cells. Because Forms/3 follows lazy evaluation rules, only those cells whose values are required in order to display correct values for any visible cells will be evaluated at a given time. Also, rather than defining an atomic value for the cell, a formula defines a temporal vector, which is a series of values taken by the cell over the course of logical time [Burnett and Ambler 1994]. In Forms/3, logical time is the language-defined dimension that is used to maintain distinct and synchronized values for every cell in a program. Because of these temporal vectors, Forms/3 is able to maintain referential transparency, even to the extent that time-based programs can run both forward and backward through logical time. Formulas can refer to the values of other cells, both at the current logical time and at earlier times. The operations that are used in this example are described here. See [Hays and Burnett 1995] for a more complete introduction.

if/then/else

The conditional expression is analogous to the Lisp "(if test thenClause elseClause)," and allows nesting in exactly the same manner. It returns the result of the then clause if the test is true, otherwise it returns the result of the else clause. In Forms/3, the else clause is optional, and the failure of the test in an if/then expression results in no new value being defined.

earlier/initially/until

The earlier expression provides reference to the value of a cell during the previous moment of logical time, thus allowing non-destructive iteration. The optional initially modifier allows the programmer to define a value for the cell at starting time, and the until modifier allows the programmer to specify that, when the test in the until clause becomes true, the cell's value applies for all future moments in time. For example, if a cell named "foo" has the formula: "earlier (foo + 1) initially 1 until (foo > 5)," it would count from 1 to 6, and its value at all later times would be 6.

fby

Fby specifies an initial value for a cell and its value after a start time. For example, "1 fby 2" would define a cell as having the value 1 at time 1, followed by the value 2 at all later times.

matrixSearchRowWhere and matrixSearchColWhere

These expressions allow the programmer to search through a matrix for a specific value. If it is found, its row or column is returned.

error?

This expression returns TRUE for values of type error, and FALSE otherwise.

Matrix access

Matrices are accessed using the syntax "aMatrix[row@col]," where aMatrix is the name of the matrix, which is indexed by the values of row and col. The values of row and col can be integers or cell names. It is also possible to specify "aMatrix[i@j]," which is the element of aMatrix that has the same row and column indices as the referring cell. Here, i and j are reserved words.

3. The Turing Machine Simulator

This Turing machine simulator includes three separate forms in its program: The form TuringProgram (Figure 1) contains all of the user-modifiable cells that define the properties of the Turing machine to be modeled. The form TuringCompute (Figure 2) carries out the operations which translate the Turing machine definition in TuringProgram into behaviors of TuringInterface (Figures 3, 4, and 5). The form TuringInterface has a matrix for user input, as well as an animated display of the machine tape.

This demonstration Turing machine is programmed (via TuringProgram in Figure 1) to take a string of binary digits as its input, and the result is that string concatenated with itself. That is, it performs the computation:

Its method of carrying out this program can be summarized as follows:

1. Traverse the original string from left to right, replacing each "0" with an "x" and each "1" with a "y".
2. Return to the left end of the string, and replace the first letter with its corresponding numeral.
3. Move to the first blank to the right of the string, and write the same numeral as written in step 2.
4. Repeat from step 2, until only numerals are present in the final string.

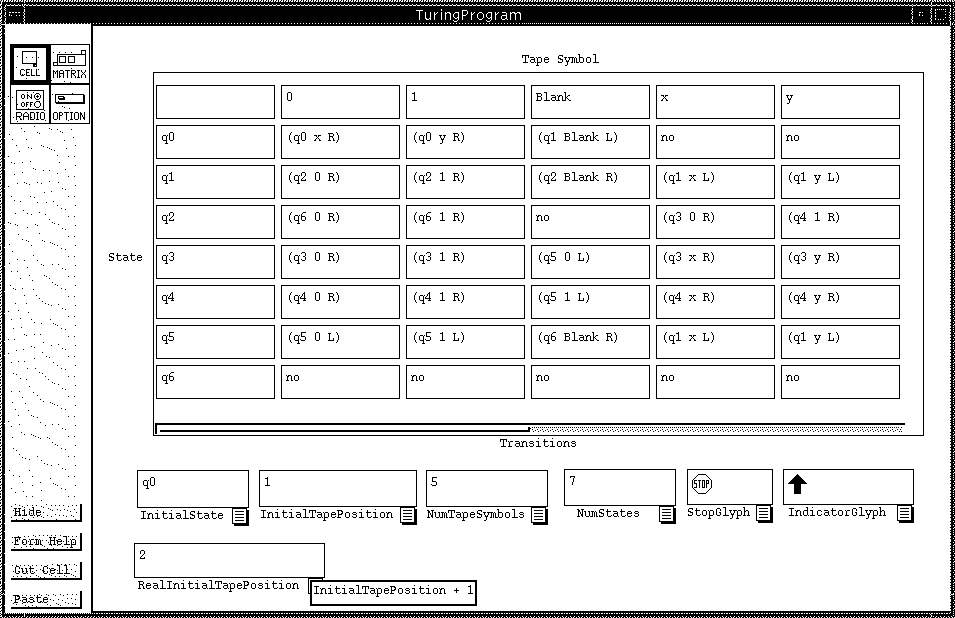
Figure 1: TuringProgram defines the transitions, states, and tape symbols used by the simulator. In the Transitions matrix, the first row is the index of tape symbols, and the first column is the index of states. The proper transition is found by accessing the matrix element found in the row containing the current state as its index, and in the column containing the current tape symbol. The transitions are expressed as triples, consisting of the next state, the symbol to write on the tape, and a direction to move. Every cell on this sheet (except RealInitialTapePosition) is meant to be edited by the user to change the program given to the Turing machine. Thus, all of these cells have constant formulas (e.g. "3"). RealInitialTapePosition is an interface convenience, which is meant to hide the fact that the actual operation of the Turing machine places a "Blank" in the first Tape position.

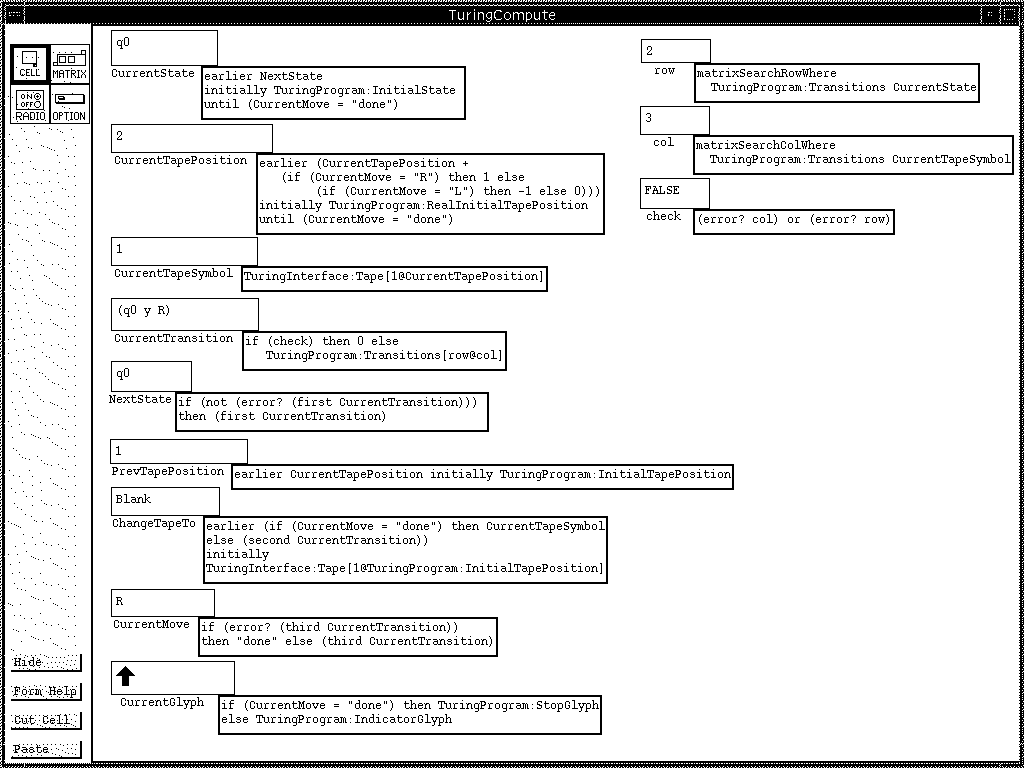
Figure 2: TuringCompute performs calculations necessary to operate the interface. CurrentGlyph is the graphic that is used as a pointer in the animation, and its appearance depends on whether or not the calculation is finished.

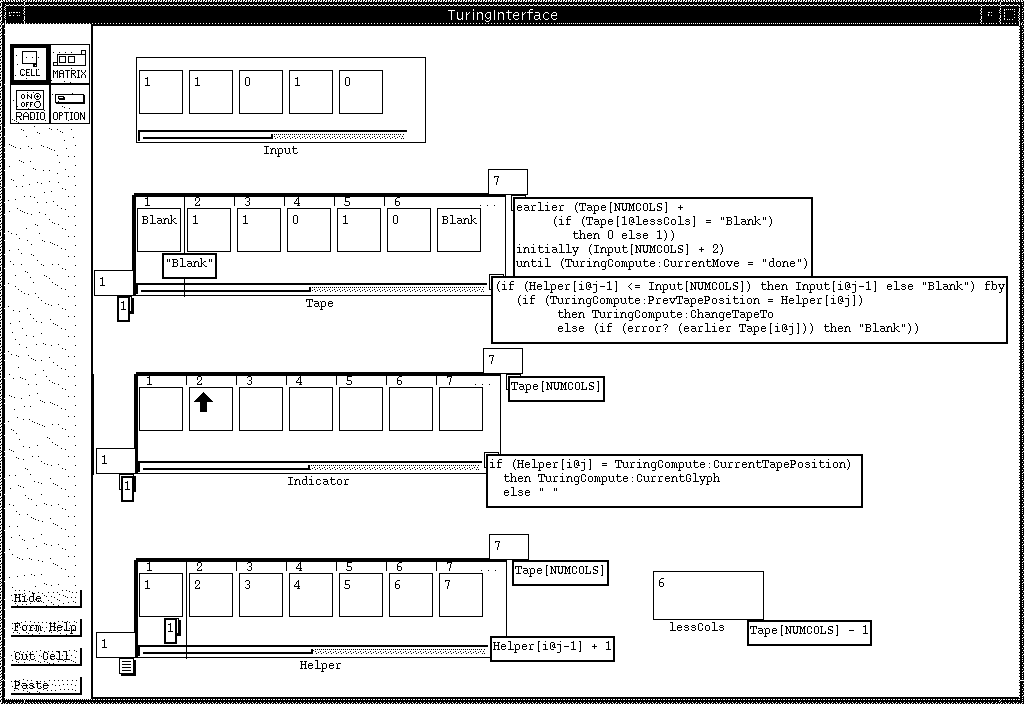
Figure 3: TuringInterface: initial state of the interface, showing the calculations used to display the tape and the animation. The Input matrix can be modified by the user. All cells are shown, and the Tape and Indicator matrices have been moved farther apart than normal to allow room for displaying all formulas.

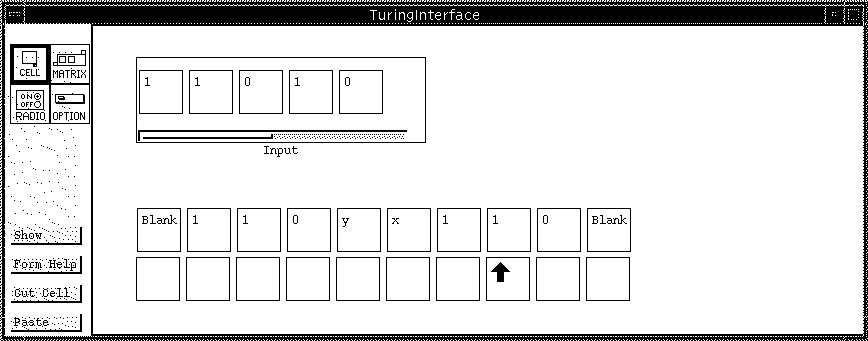
Figure 4: TuringInterface: the interface as seen by the user, at an intermediate stage of calculation. While Figure 3 showed all of the implementation details of this form, this figure shows only the features visible to the user. The cell lessCols and the matrix Helper have been hidden, as have the formula tabs for everything and the borders and labels for the Tape and Indicator matrices.

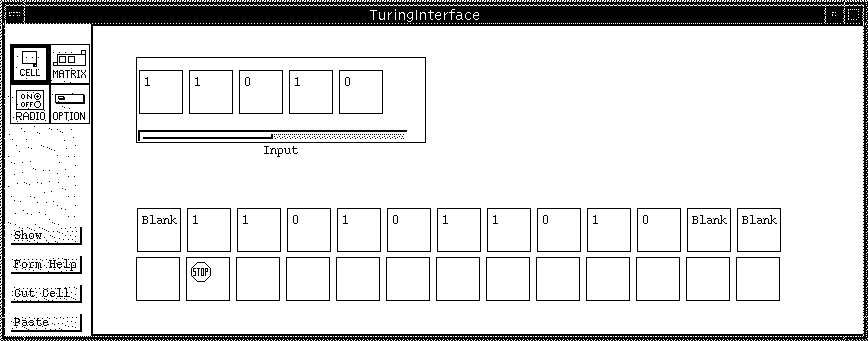
Figure 5: TuringInterface: final state of the interface.

4. Conclusion

This demonstration shows that the VPL Forms/3 can simulate the operation of a Turing Machine. Therefore, Forms/3 has computational power equivalent to that of a Turing machine.

References