

This exercise is concerned with building surfaces for computer graphics. It will
introduce various types of parametric surfaces.
Procedure:
First you will need to download two files. To do this, click on each of the filenames shown below. When the text window opens, use the "save as" option to put the file in your own directory. Name each file with the same name as shown below.
After downloading the files, start DX then open and execute parametric.net. Each module (when opened) has a one-line explanation of its function. One of the Compute modules performs the main operation of mapping a 2D grid to 3D coordinates to make the parametric surface. (The others just produce pi and produce the variables [v,w].)
Quadric surfaces: Modify the Compute in Parametric.net to produce a unit sphere. Use another Compute module to convert the sphere to a "superquadric". That is, if the vector [x,y,z] is a quadric surface, then [x,y,z]^n is a superquadric surface, where the power of a vector just means the power of each term. Try values of n from .2 to 10 or so. You will need to handle negative values of x, y, and z in the compute. Make the value of n set by an interactor. The two images below show a sphere modified by n=.3 and n=3 respectively.


Figures of rotation: Modify the program to produce a figure of rotation given by cylinder radius r=abs(w)+.1 where w is the axis of the rotation. Modify the program to produce a figure of rotation which approximates the shape of a drink bottle. Two bottles from spring 1995 are particularly elaborate.
Note that the form a?b:c used in a compute module is a conditional. If a is not equal to zero, then do b, else do c. This allows arbitrary functions to be constructed. For example, try r=0.2+(w>=0.4?(w-0.4):0.0) to make a funnel.

Modify the original Parametric.net program to convert the torus into a spiral spring with four complete turns. Animate the spring so that one end of the spring remains fixed and the other end undergoes simple harmonic motion. The spring should not pass through itself and the motion should repeat every 16 frames. Model a sphere which moves sinusoidally with the end of the spring and appears to be attached to the spring. One frame of an animation is shown below.
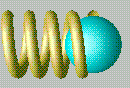
Bugs as of 3/7/95
Copyright (1995) by Cornell University. Copyright Statement