program2.tar contains my
solution to the previous assignment, as well as implementations of
Jack's Car Rental, Russell's 4x3 world, and the Windy Gridworld.
First, let me say a few things about the previous assignment. I discovered that prioritized sweeping does not provide ANY benefit on Jack's Car Rental. In fact, I found it quite difficult to measure any benefit from doing value iteration rather than just executing a random policy on this problem! The improvement is not very large.
When I compared prioritized sweeping with value iteration on the 4x3
maze, I found that 4x3psweep -n 0 performs only 280 Q
backups before convergence, whereas 4x3vi performs 396 Q
backups. However, this is probably not a fair comparison, bcause
although I'm using the same value of epsilon in both cases, the
epsilon's mean different things. The original motivation for
prioritized sweeping was to improve performance during the
stochastic planning process. In other words, suppose we compared the
greedy policies after performing, say, 100 Q backups. Which method
would be better? To measure this, I have implemented a new member
function, MonteCarloEval and arranged for it to be called
after every MCinterval Q backups. This function performs
MCNSteps of simulated execution and computes the total
discounted reward received over those steps and prints it out. There
is a global variable MCpolicy, which specifies which
policy should be executed. I have set this variable to 0, which means
that the greedy policy should be executed, but you can also set it to
1, which causes a random policy to be execute.
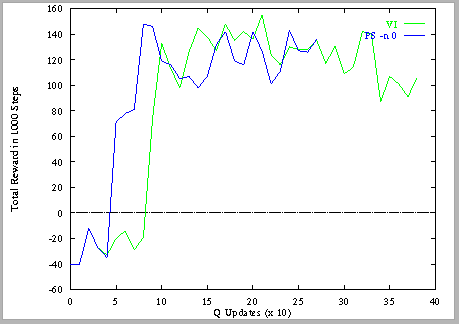
The graph below shows the online performance of the two algorithms.

We can see that Prioritized Sweeping achieves good performance sooner. If we set the epsilon for Prioritized Sweeping to be even bigger (e.g., 0.1 instead of 0.01), then it achieves better performance even sooner. In effect, by using a large value for epsilon, we are doing only the important backups. This effect is even stronger in the Windy Gridworld, because value iteration takes a long time to propagate information from the goal back to the start state, whereas prioritized sweeping is much more direct. Please construct a graph similar to the one shown above comparing prioritized sweeping (with -n 0) and value iteration.
You may be interested to see a trick that I used to handle duplicate entries within the priority queue. I created a global counter to count the number of Q backups that had been performed. Each time I pushed an item onto the priority queue, that item was time-stamped with the current value of that counter. In addition, each time I updated a Q value, I time-stamped that value with the counter. In the main loop of prioritized sweeping, each time I pop an item off the stack, I check the Q(s,a) value that it wishes to update to see if it has been updated more recently than the stack item. If so, I discard the stack item. This was essential to getting this code to run in a reasonable amount of time. It wastes space on the priority queue, but it is much easier to implement than a priority queue that supports hashed access to the elements and updating of priorities.
In this assignment, you will implement two online algorithms, SARSA(0) and Q. These methods are model-free: they do not learn or use models of P(s'|s,a) or R(s'|s,a). The implementation for these two algorithms is exactly the same except for the Q update equation, so I suggest that you define one function and pass a flag that indicates whether you want to do Q learning or SARSA.
Your program should permit the following to be specified at the command line (or interactively):
Every time your program completes a trial, it should print out the number of primitive actions (which you should keep track of using the global variable ActionCounter) and the number of episodes. This will make it possible for you to create a plot like that of Figure 6.11. Note however, that I have not been able to reproduce that particular plot. The text is a bit confusing about the definition of the domain, and I have made some changes to make it more interesting. The main change is that I give a reward of 20 for reaching the goal.
Turn in the following: