Return to Home Page
WHAT TO DO NEXT:
USING THE PROBLEM STATUS TO DETERMINE
THE COURSE OF ACTION
David G. Ullman and Derald Herling Bruce D'Ambrosio
E-mailUllman
Department of Mechanical Engineering Department of Computer Science
Oregon State University Oregon State University
Corvallis, Oregon, 97331 Corvallis, Oregon, 97331
ullman@engr.orst.edu dambrosi@cs.orst.edu
I. Introduction
This paper addresses decision making support for teams faced with solving problems with
numerous potential alternative solutions(1). These types of problems are common in everyday life
and especially prevalent during the design process. Usually, not everything is known or knowable
about the alternatives and the criteria with which the alternatives are evaluated. The goal is to
choose an alternative based on this incomplete information. In this paper, we will show that, at
any time during deliberation, the state of the designers' knowledge (i.e their information) about
the alternatives and criteria directly determines what activities to undertake to make a decision
with confidence.
During the solution process, the decision makers are repeatedly asking three questions:
"What is the best alternative?"
"Do we know enough to make a decision yet?"
and " What do we need to do next to feel confident about our decision?"
Traditional decision support tools only address the first of these three questions. While the latter
questions have been extensively investigated in the statistical and decision analysis communities,
little of this theoretical work has been translated into practical tools for working designers.
However, we will show that within what is known about the alternatives and the criteria there is
sufficient detail to assist in evaluating how satisfied the decisions makers are with each
alternative and to give guidance about where to spend time and money to obtain more
information.
The problems we address here are characterized by evaluating the attributes of the alternatives
relative to some criteria. These types of problems are often referred to as multi-attribute, multi-objective or multiple criteria problems. Problems of this type are a dominant activity seen during
the design of products [Stauffer 91] and business processes.
During the solution of multi-attribute problems, the decision makers strive to develop
information sufficiently complete so they can make the best possible decision. Design problems
always beg for more information. However, without exception, there is limited time and other
resources available to gather more information on which to base a decision, even though the
result may greatly affect downstream product quality, time to market and cost. This paper is
focused on how the state of a multi-attribute decision problem itself can give guidance on where
to invest resources to gather information sufficient for a decision in which the whole team is
confident.
To achieve this level of team support, this paper integrates preference and belief, the two main,
and traditionally independent components of decision theory. Preference is a model of what the
decision maker(s) care about. This is often quantified by an objective, cost or utility function.
Belief represents of the likelihood of a particular solution to the problem being favorable with
respect to a decision maker's preferences. The belief model expresses what the decision
maker(s) knows or accepts to be the basis for making the decision. This can be measured by the
knowledge about the alternatives and the confidence in them satisfying the criteria. Belief is
quantified through the use of probabilities. The model which integrates preference and belief is
based on Bayesian decision theory but, as will be seen, requires little probability estimation from
the decision makers. This work is has its foundation in recent contributions by the uncertainty in
artificial intelligence community on factored representations of probability distributions
[D'Ambrosio 96].
 The paper begins with an example problem,
Section 2. The decision making model described
here has been used to support a number of
industrial problems. One has been simplified here
to provide a thread to the concepts presented in this
paper. In Section 3 we present a description of the
characteristics of multi-attribute problems. These
characteristics lead to a Bayean model of multi-attribute problems in Section 4. This model
supports the first two of the questions posed above:
"What is the best alternative?" and "Do we know
enough to make a decision yet?". Further
development of the example problem will
demonstrate this support. The model is extended in
Section 5 to support the third question, "What do
we need to do next to feel confident about our decision?". This support uses a type of sensitivity
analysis we call "expert knowledge analysis"(2) to suggest future courses of action. This section
develops the most important contribution of this paper. The earlier material is included to set the
stage for this work. Again, the example problem will be used to show the simplicity of this
model and the value of the information developed. The paper will end with a summary and
directions for further work in Section 6. At a minimum, the most original contributions of this
paper can be appreciated by reading Section 2 and the material from Table 4 onward.
The paper begins with an example problem,
Section 2. The decision making model described
here has been used to support a number of
industrial problems. One has been simplified here
to provide a thread to the concepts presented in this
paper. In Section 3 we present a description of the
characteristics of multi-attribute problems. These
characteristics lead to a Bayean model of multi-attribute problems in Section 4. This model
supports the first two of the questions posed above:
"What is the best alternative?" and "Do we know
enough to make a decision yet?". Further
development of the example problem will
demonstrate this support. The model is extended in
Section 5 to support the third question, "What do
we need to do next to feel confident about our decision?". This support uses a type of sensitivity
analysis we call "expert knowledge analysis"(2) to suggest future courses of action. This section
develops the most important contribution of this paper. The earlier material is included to set the
stage for this work. Again, the example problem will be used to show the simplicity of this
model and the value of the information developed. The paper will end with a summary and
directions for further work in Section 6. At a minimum, the most original contributions of this
paper can be appreciated by reading Section 2 and the material from Table 4 onward.
2. An example problem
This section begins with a design problem example. This clarifies the type of problem addressed
in this paper and it will be used throughout the paper to aid in understanding the model
developed. The problem is abstracted from an actual situation.
The problem addresses the conceptual design of a bicycle suspension system for the BikeE
Corporation. This company manufactures the recumbent bicycle shown in Figure 1. The rider is
currently cushioned from road roughness by the flexibility of the cantilevered rear stay (i.e. the
rear fork) and the foam cushion. Although the current flexible stay does a fairly good job of
isolating the rider from the road, customers have repeatedly requested a more active suspension
system. There are three members of the team who will design and approve this product: Dave,
the lead engineer with formal engineering training, Paul, a second engineer with much practical
bicycle experience but little formal education, and John, the product manager and chief of sales.
In team meetings a number of concept proposals and criteria were developed. In this example
only three alternatives and three criteria will be used. Many more were developed in the actual
solution of the problem. The alternatives considered here are:
A1: Pivot the rear stay at the body and use a "Jackrabbit"mountain bike spring/damper unit.
These are available from the manufacturer as a complete unit. Only a mounting scheme will
need to be developed.
A2: Pivot the rear stay at the body and design a custom elastomeric spring/damper tuned to the
BikeE configuration.
A3. Develop a sprung seat cushion.
The bold terms are used throughout the rest of the paper as short hand notation for these
alternatives. The criteria used as a basis for evaluation of the alternatives are:
C1: The manufacturing cost per unit must be less than $15 above the cost to manufacture the
current, unsprung product.
C2: The suspension system should isolate the rider from 75% of the energy input from bumps in
the road to give riding comfort.
C3: The suspension system should visually appeal to a majority of the customers.
Although this information is very abstract and should be refined [Ullman, 96], many decisions
are made daily with such meager information. The main question faced by the team is: Which
alternative(s) should be pursued? The team must now collect enough information to evaluate the
alternatives relative to the criteria(3). For most problems, collecting complete information on
every alternative is not possible within the constraints of time and money, and thus early
decisions are based on incomplete information. Further, this information may be inconsistently
understood by the different members of the design team.
Typical exchanges during team discussions evaluating the alternatives were:
Dave "I believe that I can design an elastomeric system that will give a great ride".
Paul "A preliminary quote from the vendor has the "Jackrabbit" at $18.25 in lots of 1000
units".
John "We don't know enough about the elastomer, the Jackrabbit is too expensive and I don't
think the customers are going to like a sprung seat cushion. They will think our bike is a
tractor."
Each of these quotations has two features; an implied level of knowledge about an alternative's
attribute and a confidence statement about how well the alternative actually meets the criterion
addressing the attribute. For example, in the first quote, the comfort attribute of the elastomer
alternative is abstractly compared, by Dave, to the comfort criterion. His knowledge is not high
("I believe") about the comfort attribute of the elastomer alternative. However, he is confident it
will meet the target set by the criterion statement. These two features of alternative evaluation
are detailed in Sections 3.3 and 3.4.
Decision support for this problem was provided by software developed during the research. We
call It the Engineering Decision Support System (EDSS). A PC version is under continuous
refinement(4), and a Unix version, with reduced capabilities, is available on
http://www.cs.orst.edu/~dambrosi/edss/info.html.
3. The Characteristics of Multi-attribute Problems.
This paper addresses single issue problems characterized by the need to evaluate multiple
alternatives before arriving at a decision [Herling 95, Ullman 95]. Information about the
alternatives may be incomplete and viewed by members of the decision making team in an
inconsistent manner. Problems with these characteristics are especially prevalent during design
activities. Stauffer [Stauffer 87], in his detailed study of five designers working alone on a
conceptual design problem, found that 83% of the design activity was search rather than
deduction (i.e. if-then rules). Similar results were found in a study of architects [Akin 86]. A
characteristic of all search strategies is that specific alternatives are compared to individual
criterion in order to gain information on which to base the decision.
In general, most design problem solving activity can be viewed as the comparison of alternatives
to criterion by members of the design team. Thus, for N alternatives, M criteria and J team
members there may be N x M x J comparisons. Informal study of design teams show that the
decision space, that space defined by the alternatives and limited by the criteria, is seldom fully
explored and thus, the evaluation is incomplete. Further, it is common that the team members do
not consistently evaluate many of the alternative/criterion pairs as they have differing views and
knowledge about the problem. Issue critical to managing incompleteness and inconsistency are
detailed in the sections below.
3.1 Completeness of design space
In the design space, information describing the alternatives and criteria may be incomplete. If all
the alternatives are known and all the criteria for evaluation can be itemized (i.e. fixed), then the
problem is considered complete. In most design problems and in the BikeE example above, the
alternatives and the criteria for their evaluation evolve(5) as the discussion progresses. There is no
confirmation that either is complete even after a decision is made. The problem is open to new
alternatives and criteria. Team members seldom itemize the entire set of potential alternatives
and even when using a system such as quality function deployment (QFD) [Ullman 96] they are
never assured that they have addressed all the criteria.
3.2 Completeness of assessment
In most engineering decision making problems all the alternatives are not evaluated against all
the criteria by everyone on the design team. This is especially true if the team is multi-disciplinary. Where the completeness of the design space (Section 3.1) refers to the number of
alternatives and criteria, this characteristic focuses on the completeness of the team evaluation of
them.
When using a formalized method such as a decision matrix (often called Pugh's method and
detailed in [Ullman 96]) or formal optimization there is a need for assessment completeness.
However, consider the following from the BikeE example introduced above. After studying the
team's entire deliberation on the issue of the suspension, the coverage of the design space can be
represented as shown in Table 1.
| D= Dave
P=Paul
J=John |
Alternatives |
| Jackrabbit |
Elastomer |
Cushion |
Criteria |
cost |
D,J,P |
J,D |
|
| comfort |
P |
D |
|
| visual |
J,P |
J,D,P |
J,P |
Table 1: Design space evaluation by team members
The entire team evaluated only two of the alternative/ criterion pairs; only a part of the team
voiced opinions on many other pairs; and for two pairs, no one expressed any opinion at all. This
is often the case during design when team members have different domains of expertise and
strong feelings about some of the alternatives and indifference about others.
Completeness of assessment is often tied to the team members' predilections. There are two
types of predilection commonly shown by team members. When a team member is strongly
biased toward a particular alternative then s/he is referred to as the "alternative's champion."
When a team member expresses a particular view through weighting or ordering the criteria, s/he
is considered to have a specific view of the decision problem. All team members have a specific
view and some are champions for a specific alternative. As will be seen in the example, John
clearly expresses a marketing/management view through his heavy weighting of the cost criterion
and Paul is clearly the champion for the Jackrabbit alternative.
3.3 Knowledge about design space
In the ideal world each team member would be an expert and could evaluate how well each
alternative met each criterion with authoritative knowledge. However, this is seldom the case
and decisions are usually made with less than expert knowledge. Knowledge is a measure of the
information held by a team members about the attributes of the alternatives compared to the
criteria(6). During design activities knowledge is generally increased (i.e evolved) by building
prototypes, performing simulations (analytical and physical) or finding additional sources of
information (e.g. books, vendors, experts, consultants). Each of these activities to increase
knowledge requires time and the commitment of resources. This commitment needs to be
carefully considered as will be further developed in Section 5.
In the current implementation of the method, knowledge is communicated to the EDSS by
selection of a descriptive word which is translated into a measure of the probability of perfect
knowledge [Herling 95, D'Ambrosio 95]. In this scheme an individual with perfect knowledge
would be able to correctly answer 100% of the questions concerning the evaluation of an
alternative's attribute (probability = 1.0). At the other end of the scale an individual with no
knowledge would have a 50/50 chance of guessing correct information (probability = .5). The
following word/value combinations were generated from results of questionnaires completed by
students and engineers: expert (.97), experienced (.91), informed (.84), amateur (.78), weak (.66),
unknowledgeable (.57). Thus, someone who was an "amateur" would answer 78% of questions
correctly (probability = 0.78). Details on the survey used to find the values are in the references.
In the example problem Paul has studied the Jackrabbit system and knows a great deal about it,
but not much about the other two alternatives. Dave, on the other hand has been studying the use
of elastomers as spring elements and he also developed the idea of the sprung seat based on his
experience as a boy growing up on a farm. John is mainly knowledgeable about customer related
issues. Their self assessed knowledge(7) about the design space is shown in Table 2, a listing of
the knowledge and confidence (covered in the next section) information input into the decision
support system.
| Team Member |
Alternative |
Criteria |
Knowledge |
Confidence |
Dave
|
Jackrabbit |
cost |
Amateur (.78) |
Questionable (.42) |
| Elastomer |
cost |
Experienced (.91) |
Likely (.73) |
| Elastomer |
comfort |
Informed (.84) |
Likely (.73) |
| Elastomer |
visual |
Experienced (.91) |
Likely (.73) |
John |
Jackrabbit |
cost |
Amateur (.78) |
Unlikely (.28) |
| Jackrabbit |
visual |
Informed (.84) |
Likely (.73) |
| Elastomer |
cost |
Amateur (.78) |
Potential (.62) |
| Elastomer |
visual |
Amateur (.78) |
Potential (.62) |
| Cushion |
visual |
Experienced (.91) |
Unlikely (.28) |
Paul |
Jackrabbit |
cost |
Informed (.84) |
Potential (.62) |
| Jackrabbit |
comfort |
Experienced (.91) |
Likely (.73) |
| Jackrabbit |
visual |
Experienced (.91) |
Likely (.73) |
| Elastomer |
visual |
Informed (.84) |
Likely (.73) |
| Cushion |
visual |
Informed (.84) |
Unlikely (.28) |
Table 2: Example problem evaluation
3.4 Confidence in the evaluation
Confidence is a measure of how likely the evaluator believes that the alternative meets the
criteria. A well stated criterion measures a specific attribute of the alternative and gives an
indication of what is the acceptable performance of this attribute. However, many design criteria
are not fully represented numerically with known or even calculatable goal states. Thus,
confidence is often subjective and part of the judgement necessary to solve design problems.
In the current implementation of the method presented here, confidence is communicated to the
computer by selection from a list of descriptive words. Here confidence that the alternative
meets the criteria has probability of 1.0 and a probability of 0.0 if it is totally unlikely to meet the
criteria at all. In terms of surveyed descriptions of confidence, the likelihood of how well an
alternative is judged to meet a criterion are: Perfect (.97), Likely (.73), Potential (.62),
Questionable (.42), and Unlikely (.28). For the example problem, the team members' confidence
in each alternative are presented in Table 2. As will be shown, these confidence levels will
change as the solution to the design problem evolves.
Confidence and knowledge are the two measures of the evaluator's belief space as shown in
Figure 2. In the figure, knowledge can range from .5, a guess with 50-50 odds, to perfect
knowledge, a probability of 1.0. Confidence in the alternative's likelihood of meeting the criteria
can range from 0.0, it does not meet it at all, to 1.0, where the alternative is believed to fully meet
the goal stated in the criteria. If, for example, an alternative is compared to a criterion by a
member whose knowledge is low and is also not very sure about how well the alternative meets
the criteria, then their belief can be represented as the small circle in the figure. If the designer
performs some analysis, experiment or other research effort to improve his/her knowledge, the
increased knowledge gained can be represented by progress along either of the two arrows. If the
result of the evaluation causes a increase in confidences, the upward arrow is followed.
Conversely, a loss in confidence follows the downward path. As knowledge is increased,
confidence values migrate to 0, no confidence, or 1, complete confidence with the region A being
infeasible. Here it is important to note that the probability of satisfaction increases as the
knowledge and confidence increases and decreases as knowledge increases and confidence
decreases The mathematics for this are developed in the appendix. Thus, for the lower arrow in
the figure, work on this alternative may be halted as the potential for satisfaction is diminishing.
The upward path shows the probability for satisfaction increasing with increasing knowledge and
confidence. One goal in design is to choose alternatives for which the probability of satisfaction
increases as work is done refining it. This goal will drive the path to the upper right corner as the
project progresses. We will return to this concept in Section 5.
Also shown in Figure 2 are regions B and
C. Knowledge/confidence values in
Region B imply that the evaluator has a
religious zeal for the alternative which is
probably irrational. Likewise, values in
region C are referred to as "Eyore" values
after the character in the Winnie the Pooh
books, as the alternative is bound to be
poor even though little is known about it. 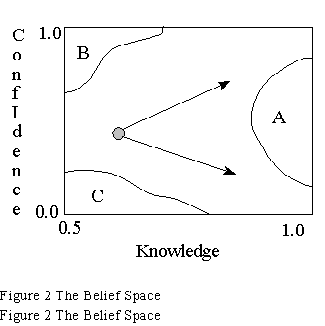
3.5 Consistency of judgement
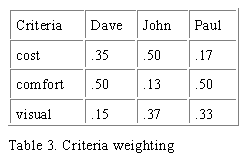 When a team is making a decision, there may be many
different viewpoints regarding the importance of
criteria, thus the preference model may vary from
member to member. If there are differing viewpoints,
then the preference model is inconsistent. We handle this inconsistency by eliciting the
weighting factors on the criteria from each team member independently. Although there are
many methods for developing weights(8) we currently elicit them directly. Weights normalized to
total 1.0 for each team member are shown in Table 3 for the example problem. Note the
inconsistency in judgement about what is important in this problem. These different weightings
will be used to give richness to the satisfaction evaluation and sensitivity analysis developed in
Sections 4 and 5.
When a team is making a decision, there may be many
different viewpoints regarding the importance of
criteria, thus the preference model may vary from
member to member. If there are differing viewpoints,
then the preference model is inconsistent. We handle this inconsistency by eliciting the
weighting factors on the criteria from each team member independently. Although there are
many methods for developing weights(8) we currently elicit them directly. Weights normalized to
total 1.0 for each team member are shown in Table 3 for the example problem. Note the
inconsistency in judgement about what is important in this problem. These different weightings
will be used to give richness to the satisfaction evaluation and sensitivity analysis developed in
Sections 4 and 5.
4. A Bayesian Model of Multi-Attribute Team Decision Problems
This section develops the mathematics behind the method of decision support. The example
problem is referred to again at the end of the section.
It may seem that the alternative/criterion representation for a decision problem is rather
simplistic and ad-hoc. However, support for this representation comes from extensive research
into modeling decision-making processes in design [Blessing 94 and Yakemovic 89]. In addition,
there is a fairly straightforward mapping to an influence diagram, as shown in Figure 3. It is this
graphical representation from which our model of argumentation is derived [Shacter and Fung 90
and D'Ambrosio 94].
Figure 3 contains representations of the alternatives available, the criteria by which alternatives
will be judged, the relative importance of the criteria, and design team member opinions on the
likelihood that various alternatives meet various criteria. Section 4.1 defines the semantics of the
diagram, 4.2 documents the inference procedure for evaluating alternatives is documented, and
4.3 suggests methods for identifying useful information gathering actions(9).
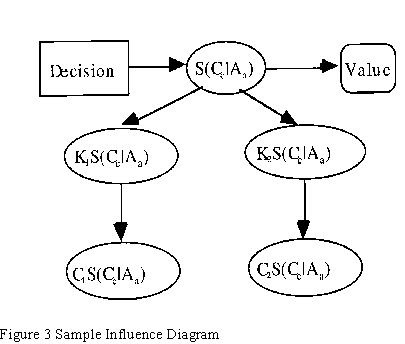
4.1 Diagram Semantics
In Figure 3 the box labeled "Decision'' takes as values the alternatives for resolving the issue
represented by the diagram. The circle labeled S(Cc|Aa) represents the satisfaction of criterion Cc
given alternative Aa and will be called a satisfaction node. While we show only one, there will be
one for each alternative/criterion combination. In our initial explorations we allow only Boolean
({yes, no}) satisfaction levels. Therefore, knowledge and confidence are about the certainty that
the alternative will satisfy the criterion, not the degree to which satisfaction is achieved(10). The
pair of two node chains hanging from S(Cc|Aa) represent opinions posted by participants. There
can be any number of such chains hanging from each of the S(Cc|Aa) satisfaction nodes, one for
each opinion. The higher of the two circles represents the state of participant knowledge about
the ability of the alternative to meet the criterion, and the lower is a diagram artifact used to
encode probabilistic evidence. The upper node (we will call this a knowledge node) takes the
same values as the original satisfaction node, namely {yes, no}. We will denote these nodes as
KpS(Cc|Aa), where a is the specific alternative being addressed, c is the criterion, and p is the
participant. The lower node takes a single value, true.
The conditional probability of the knowledge node given the actual satisfaction has two degrees
of freedom. We reduce this to a single degree by assuming symmetry to simplify knowledge
acquisition. That is, we assume
P(KpS(Cc|Aa)=yes|S(Cc|Aa)=yes) = P(KpS(Cc|Aa)=no|S(Cc|Aa)=no).
This single degree of freedom is the knowledge the participant has about the alternative/criterion
pair, because this single parameter encodes how accurately the participant's belief reflects the
actual world state. The complete distribution for a knowledge node, then, is:

We allow Kc,a,p to range between 0.5 and 1.0, where 1.0 represents perfect knowledge and 0.5
represents complete ignorance, and use the textual scale described earlier to acquire the Kc,a,p
value.
We will refer to the lower node as the Confidence node, Cp(S(Cc|Aa). The confidence node has
only one value and all that matters is the ratio of the probabilities for that value given KpS(Cc|Aa).
We acquire this as the "probability that the alternative will satisfy the criterion, given the
participants state of knowledge" That is, we treat the participant as a making a noisy or soft
observation (report) on his or her belief. We encode this as a pair of numbers constrained to sum
to one, as follows:
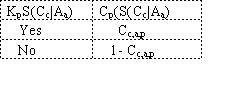
Note that this model assumes uncorrelated evidence from team members, and thus is optimized
for multi-disciplinary teams. While modeling correlation among opinions is straightforward, it is
an extra burden on the team which outweighs the advantages in most situations.
4.2 Alternative Evaluation
Given the above semantics, the expected value of an alternative is:
EV(Aa) = cV(Cc)P(S(Cc|Aa)=yes)
where
P(S(Cc|Aa)=yes) = p (Cc,a,pKc,a,p + (1- Cc,a,p)(1- Kc,a,p))
and is a normalization factor:
= 1/(p (Cc,a,pKc,a,p + (1- Cc,a,p)(1- Kc,a,p))
+ p (Cc,a,p(1- Kc,a,p) + (1- Cc,a,p)Kc,a,p))
The alternative with the highest satisfaction value is the "best" as judged by the team. This
answers the first question "What is the best alternative?". However, looking at this single value
is not recommended. First, the difference between the most satisfactory and the other
alternatives must be considered especially in light of the qualitative nature of the information on
which the satisfaction was calculated. Second, there is the question of sufficient knowledge to
make a decision, or as stated in the second question "Do we know enough to make a decision
yet?" Obviously, increased knowledge will improve the confidence in the decision, but the
above analysis can not yet answer the second question. Thus, the analysis will be extended in
Section 5.
4.3 Methods for Evaluation
Using the model presented above, the team's evaluation for this problem is shown in Table 4.
The information input into the program, Tables 2 and 3 and the results of the evaluation, Table 4
are all entered in a database. As will be seen, this information is the first step in the development
of a history for the design decision.
|
Individual Evaluator |
Team Evaluation Using: |
| Alternative |
Dave |
John |
Paul |
Dave's
weights |
John's
weights |
Paul's
weights |
| Jackrabbit |
.48 |
.50 |
.67 |
.61 |
.59 |
.68 |
| Elastomer |
.67 |
.55 |
.55 |
.71 |
.77 |
.73 |
| Cushion |
.50 |
.43 |
.45 |
.45 |
.39 |
.40 |
Table 4: Expected value results
There are a total of six different sets of satisfaction results developed and shown in Table 4. The
first three columns show calculations based solely on the information input by each individual.
As can be seen, Dave has said nothing about the cushion so his satisfaction is .50, neither good or
bad. Both John and Paul show less than neutral satisfaction for this alternative. Dave is strongly
in favor of the elastomer and Paul and John are just barely above neutral for it. Paul likes the
Jackrabbit but there is little other support for it. Using a method like a decision matrix or even
the method proposed here but only applied to each individual, this is the only information on
which to base a decision. With this analysis, David likes the elastomer, Paul the Jackrabbit and
John is indifferent. These results are not very conclusive. But, the method developed in this
paper allows us to go far beyond this point.
The second set of three columns are calculations of satisfaction values for the combination of all
the team members belief (i.e. the total knowledge/confidence assessment by all the team
members), based on each members judgement (i.e. weightings in Table 3) about criteria
importance. In other words, the column labeled "John's weights" is based on the knowledge and
confidence of all three team members, but it is strongly skewed toward cost and visual appeal,
the criterion John thought most important in Table 3. Meanwhile, the column with "Paul's
weights" is strongly skewed toward rider comfort, commensurate with what he thought most
important. Note that, regardless of whose judgement is used regarding the importance of the
criteria, the cumulative effect is to strengthen the satisfaction in the elastomer and weaken that
for the sprung seat. This is due to the multiplicative effect of the algorithm. There appears to be
some weak consensus that the elastomer is the best alternative. Should all work be aimed to
refine it and drop work on the other alternatives?
The goal is not only to choose an alternative, but also to develop a consensus among the team
members in support of the choice. If there is disagreement within the team, consensus can be
reached by: 1) Gathering more information to increase the team members' knowledge about the
alternatives. Better knowledge will increase the confidence in some alternatives and reduce it in
others. This path toward consensus changes team member's belief model. 2) Negotiating the
weighting of the criteria. This path toward consensus changes team member's preference model.
A key point is to note that it is not essential to have consensus on the preference model (i.e. the
criteria weightings) in order to have consensus on the assessment of the alternatives. Consider
that in Table 3 each team member has a different view about what is important with John's view
strongly biased toward the significance of cost, and Dave and Paul toward comfort. However,
Dave and Paul do not agree on whether cost or visual properties are second most important.
None-the-less, the results in Table 4 show that, regardless of which team member's preference
model is used, all result in the same assessment of the alternatives. Specifically, the team
evaluations in Table 4 are all based on the knowledge/confidence assessments made by all the
team members in Table 2. This data represents each team member's belief about the alternatives.
Using Dave's weighting of criteria importance for example results .71 satisfaction in the
elastomer, .61 in the Jackrabbit and .45 in the cushion. Using the other team member's
weightings yields the same ordering with a maximum of 11% difference in actual satisfaction.
Since there is no disagreement in the ranking, further work on the problem can be based on an
average of the results.(11) This average shows a satisfaction of .74 in the elastomer, .63 in the
Jackrabbit and .41 in the cushion.
Disagreement in the rankings requires two conditions to occur: 1) The criteria weights between
team members must be different and 2) There must be small differences in the team aggregate
knowledge/confidence evaluation of the alternatives. Clearly, if the team believes one alternative
is much better than the others across many measures then the difference in criteria weighting will
have no effect on the selection of that alternative. Often the mere itemization and discussion of
the criteria will help encourage convergence of criteria weights [Edwards 77, Yakemovic 89]. If
there is disagreement after reasonable work to unify the team view, then the strategy must be to
improve the knowledge about the critical attributes of the alternatives.
The above analysis answers the first question posed in the introduction, "What is the best
alternative?". Current there is consensus in support of the elastomer, but it is not very strong. It
is obvious that there is little support for the cushion idea. But, should it be eliminated? Very
little information was input about it. Should the Jackrabbit be eliminated also? Is there some
activity that could be done that will confirm the decision to drop the cushion, and possibly also
the Jackrabbit, in favor of the elastomer? Is there enough information here to answer the second
and third questions, "Do we know enough to make a decision yet?", and "What do we need to do
next to feel confident about our decision?" After all, satisfaction in the elastomer is not really
very high (.74). There is much more to be learned from the data already collected.
5. Expert knowledge
In the previous section we showed how eliciting the team members' knowledge and confidence
about alternative/criterion pairs is the basis for generating very useful information that supports
decision making. In this section we will extend the analysis to give the team guidance about
what to do next.
The decision analysis above was based on very preliminary data. There is usually not enough
time or other resources to gather the needed information for the team to make decisions with
high, unanimous confidence. One challenge faced by the design team is to decide which
alternatives to eliminate from consideration and, for those remaining, which alternative/criterion
pairs to further explore (i.e. which attribute(s) of which alternative(s) to refine and/or measure
more effectively). Exploration can come in terms of developing analytical or physical models,
obtaining previously developed information or hiring consultants to supply the needed
information. Regardless of source, this need for information creates a sub-problem within each
design problem. Namely, under the constraints of time, current knowledge and resources to
develop increased knowledge, what research should be undertaken to render a decision. In terms
of the knowledge/confidence diagram, Figure 2, when can the design team eliminate an
alternative from consideration as its odds of satisfaction are so low compared to other alternatives?
 Our approach to is to aid the team in
planning what to do next is to compute
value of further exploration of each
alternative/criterion pair. This is
accomplished by calculating
EV(Decision | S(Cc|Aa))=yes. This is
found as it was for EV(Decision), but
with a pair of nodes added indicating
perfect knowledge and confidence that
alternative a will satisfy criterion c
(K=1.0, C=1.0). This perfect
knowledge calculation clearly shows the
highest satisfaction achievable if the
knowledge in each of the
alternative/criterion pairs is as high as it
can be. Another way to look at this
calculation is that it is as if a new team
member was added to the team. For
each attribute of each alternative this person is "the" expert and has confidence that the
alternative in question perfectly meets the criterion. This calculation shows how this person
would change the satisfaction and possibly the team's decision.
Our approach to is to aid the team in
planning what to do next is to compute
value of further exploration of each
alternative/criterion pair. This is
accomplished by calculating
EV(Decision | S(Cc|Aa))=yes. This is
found as it was for EV(Decision), but
with a pair of nodes added indicating
perfect knowledge and confidence that
alternative a will satisfy criterion c
(K=1.0, C=1.0). This perfect
knowledge calculation clearly shows the
highest satisfaction achievable if the
knowledge in each of the
alternative/criterion pairs is as high as it
can be. Another way to look at this
calculation is that it is as if a new team
member was added to the team. For
each attribute of each alternative this person is "the" expert and has confidence that the
alternative in question perfectly meets the criterion. This calculation shows how this person
would change the satisfaction and possibly the team's decision.
Similarly, we also compute EV(Decision | S(Cc|Aa))=no, the situation with c (K=1.0, C=0.0).
Here the expert has told the team that there is no way the alternative can meet the criteria and so
the lowest possible satisfaction is calculated.
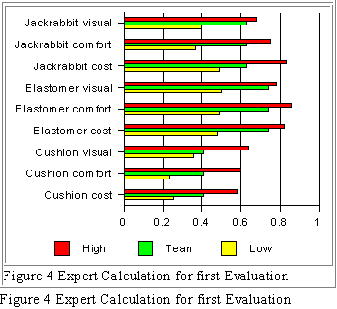
Results of these calculations for the example problem are shown in Figure 4. Here, the "team"
values are those for the average weightings in Table 4(12). The change in this satisfaction for
perfect knowledge, and high and low confidence is shown for each alternative/criterion pair.
For the Jackrabbit, the average satisfaction was calculated as .63. This is repeated as the central
bar for each trio of bars in Figure 4. In reaching this value, Dave and John only felt "amateur"
about the cost and felt that it was questionable or unlikely to meet the criteria. Paul was
"informed" and felt that the Jackrabbit had potential of costing < $15. If they knew the cost of
the Jackrabbit exactly and it was less than $15 (i.e. the criteria was perfectly satisfied) the
satisfaction in Jackrabbit may go as high as .83 as shown in Figure 4. This assumes that all other
evaluations remain unchanged. This value, .83, is greater than the satisfaction in the elastomer,
.76. In other words, before eliminating this alternative, Paul, its champion, should develop better
cost data and present it to the team, this additional information may render it a more satisfactory
solution than the elastomer. Also shown in Figure 4 is:
* If Paul's study of the cost confirms Dave's and John's belief that it does not meet the criteria,
then the satisfaction in the Jackrabbit may fall as low as . 49, reflecting the low confidence
shown during the original evaluation.
* Effort spent on improving knowledge about the Jackrabbit's performance will only have
limited payoff at this time with the maximum possible satisfaction of .75. Although this is
higher than that for the elastomer, the difference is not significant.
* No amount of work on the Jackrabbit's visual appeal will make it the first choice of the team.
This reflects the relatively strong positive evaluation given this alternative during the original
evaluation and the relatively low weighting (.28) given this criteria by the team.
* Improving the knowledge and confidence in the elastomer relative to any of the criteria can
increase satisfaction in this alternative, however the information in Figure 4 shows the greatest
potential is in adding knowledge about its ability to provide rider comfort. Failure of
experiments or analysis to show rider comfort could also eliminate it from consideration (i.e.
satisfaction less than the Jackrabbit).
* For the sprung seat cushion which had very little information entered in the original evaluation,
this sensitivity analysis shows that collecting information about it can only have a limited effect.
No single evaluation can give it higher satisfaction than either of the other alternatives.
However, if two of the criteria were to be evaluated with perfect knowledge, and both resulted in
the cushion fully meeting the criteria, then the cushion may be worth considering. Research on
the manufacturing cost can increase the satisfaction by .27 (high - team, .58-.41), comfort can
increase it .19 and visual .23. Note that the sum of the current team value plus these differences
equals unity ( .41 + .27 + .19 + .23 = 1.0). Thus, the team can pick two or three alternative
attributes to gain knowledge about. The increased knowledge may allow the satisfaction to be as
high as .83 (.41 + .19 + .23).
It is important to realize that these high and low scores only give the limits for perfect
knowledge. They do tell what the team will actually believe about the alternative after the
increased knowledge. Consider the following.
Based on the results above, the team decides that Paul needs to collect better information on the
cost of the Jackrabbit. In quotes from the vendor he finds that if they buy sufficient quantity and
if they can develop an inexpensive mounting for the system, the cost will be just below the target
of $15. He reports this information to his colleagues. Based on this report, all three now have
improved knowledge about the cost of the Jackrabbit and have new confidence in its ability to
meet the cost criterion. These new evaluations are reflected in Table 5.
|
Knowledge |
Confidence |
|
old |
new |
old |
new |
| Dave |
Amateur (.78) |
Informed (.84) |
Questionable (.42) |
Likely (.73) |
| John |
Amateur (.78) |
Informed (.84) |
Unlikely (.28 |
Potential (.62) |
| Paul |
Informed (.84) |
Experienced (.91) |
Potential (.62) |
Likely (.73) |
Table 5. Reevaluation with new information about the cost of the Jackrabbit
Based on the new information, Dave and John both felt informed about the cost, but their
judgement about it differed. Dave felt that it was likely that he and Paul could develop an
inexpensive mounting system to keep the cost below $15 regardless of quantity purchased. John,
was not so optimistic. Paul, on the other hand, was encouraged.
Based on this information, the decision support system recalculated the data (updated the
information in Table 4) and found the results shown in Table 6.
|
Team Evaluation Using: |
| Alternative |
Dave's
weights |
John's
weights |
Paul's
weights |
| Jackrabbit |
.75 |
.79 |
.75 |
| Elastomer |
.71 |
.77 |
.73 |
| Cushion |
.45 |
.39 |
.40 |
Table 6: Expected value results based on new information
 The average satisfaction calculation for
the Jackrabbit is now up to .76 while
that for the other two options remains
unchanged. Notice that the .76 < .83
(the perfect knowledge with high
confidence estimate). This is because
the team members were not convinced
they were experts nor that the
alternative fully met the criterion. The
satisfaction results show that the team
as a whole, and each individual, now
has higher satisfaction with the
Jackrabbit than with the elastomer, but
not by much. So, there are now two
candidates and the question, "What do
we do next?"
The average satisfaction calculation for
the Jackrabbit is now up to .76 while
that for the other two options remains
unchanged. Notice that the .76 < .83
(the perfect knowledge with high
confidence estimate). This is because
the team members were not convinced
they were experts nor that the
alternative fully met the criterion. The
satisfaction results show that the team
as a whole, and each individual, now
has higher satisfaction with the
Jackrabbit than with the elastomer, but
not by much. So, there are now two
candidates and the question, "What do
we do next?"
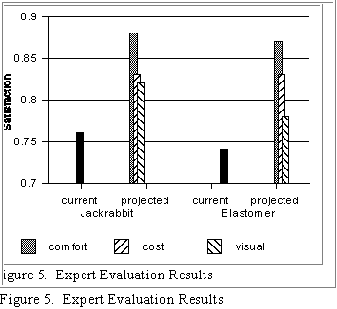
The results of the expert calculations for
this new situation are shown in Figure
5. This is the same type of information as shown in Figure 4, but presented in a different format.
Only the results for an expert with high confidence are shown here. As can be seen, both
alternatives currently have about the same average satisfaction levels. Increased knowledge
about the comfort of both of these can greatly increase the satisfaction, or, if the results of this
increased knowledge are unfavorable, decrease it. Thus, the "what to do next" question posed
above encourages developing better knowledge about the comfort of the two options. This
knowledge may result in a clear indication of which option to eliminate from consideration.
Based on this result, Dave and Paul do some analysis and experiments and report their results
back to the team. After digesting these results the team members reevaluate them as shown in
Tables 6 and 7.
|
Knowledge |
Confidence |
|
old |
new |
old |
new |
| Dave |
- |
Experienced (.91) |
- |
Likely (.73) |
| John |
- |
Informed (.84) |
- |
Likely (.73) |
| Paul |
Experienced (.91) |
Experienced (.91) |
Likely (.73) |
Perfect (.97) |
Table 6. Reevaluation with new information about the comfort of the Jackrabbit
In Table 6 the reevaluation of the Jackrabbit's performance leaves Paul feeling that he still isn't
an expert but his confidence is greatly increased. John has gone from no input at all to feeling
informed about the concept and having some confidence in its potential. Dave, who worked with
Paul to evaluate the Jackrabbit is not as optimistic as Paul.
For the elastomer, Table 7, the experiments and analysis did not go well. Dave, the elastomer's
champion feels his knowledge has increased but he is less confident in its potential to give the
rider the desired level of comfort. Now Paul and John are informed, but not encouraged by
Dave's results.
|
Knowledge |
Confidence |
|
old |
new |
old |
new |
| Dave |
Informed (.84) |
Experienced (.91) |
Likely (.73) |
Potential (.62) |
| John |
- |
Informed (.84) |
- |
Questionable (.42) |
| Paul |
- |
Informed (.84) |
- |
Potential (.62) |
Table 7. Reevaluation with new information about the comfort of the Elastomer
The results of this reevaluation are shown in Table 8. This evaluation clearly shows the
Jackrabbit is now the preferred alternative.
|
Team Evaluation Using: |
| Alternative |
Dave's
weights |
John's
weights |
Paul's
weights |
| Jackrabbit |
.89 |
.83 |
.89 |
| Elastomer |
.70 |
.76 |
.72 |
| Cushion |
.45 |
.39 |
.40 |
Table 8: Expected value results based on new information
about the Jackrabbit and Elastomer
The expert evaluation in Figure 6 shows that the elastomer does not look good compared to the
Jackrabbit. First, the satisfaction in the Jackrabbit is high and can be raised with more work on
the three attributes measured by the criterion. For the elastomer, the best chance to raise the
satisfaction is through study of comfort, but recent work on this attribute of the elastomer has
shown a loss in confidence. Thus, the team now felt confident that the Jackrabbit was the best
alternative and so all future work was directed toward this concept.
While performing the evaluation described above on the instantiation, EDSS, each new
alternative/criterion evaluation was captured as a record in a database. Although not described
here, each new entry also contained
information on the 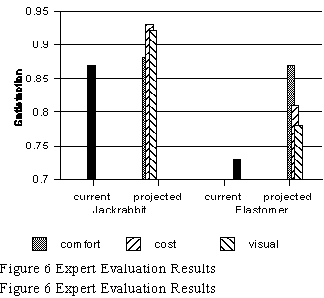 rationale for each new
record. This data base provides a design
history of the evolution of the information
and the rationale for the decisions made.
rationale for each new
record. This data base provides a design
history of the evolution of the information
and the rationale for the decisions made.
In reconsidering the questions posed in the
introduction, knowledge about the
alternatives has now risen to the point that
all three can be answered with confidence.
It is clear that the Jackrabbit is the "best"
alternative and the entire team has
confidence in this selection. It is also clear
that all future work should be on the
Jackrabbit, because no amount of effort is
likely to change the decision to select that
alternative.
6. Conclusions and Suggested Future Courses of Action
This paper has presented an overview of a methodology for supporting the evaluation of multi-attribute decision problems. This method has developed from research in engineering design
decision making and decision theoretics. It has been implemented in a computer program called
the Engineering Decision Support System, EDSS. There are three unique features integrated in
this work:
1. The methodology supports decisions through taking into account team members belief and
their preference. To the authors' knowledge, this is the first research to combine these two
aspects of traditional decision theory research.
2. The methodology provides a new way to determine a decision's sensitivity to increased
information developed through analysis, experimentation or other activity. This clearly show
potential benefit in a cost/benefit analysis.
3. The methodology takes into account and records the evolution of information which is a
natural part of design. This is essential for developing a design rationale or intent system.
In preliminary tests this implementation has shown support for the decision making process in
the following ways:
1. It directly supports the formalization and documentation of the problem elements (i.e. issues,
alternatives, criteria, criteria importance, knowledge and confidence). Earlier studies [Rittel 73,
Edwards 77, Yakemovic 89, Blessing 94] has shown that this alone has benefit.
2. It generates a series of team satisfaction values based on constructs of the input information.
These values show individual satisfaction and combined team evaluations all based on a well
accepted mathematical model. Experiments with EDSS has shown improved team productivity
[Herling 97].
3. Expert evaluation, a form of sensitivity analysis, gives clear direction on what to do next with
no additional information from the team members. This analysis shows the potential for
increased (decreased) satisfaction with knowledge increased to the expert level.
4. Changes in the evaluation of the alternative/criterion pairs are recorded in a database which
acts as a history of the decision making process. This history records the evolution of the
decisions of the design team. Further, the PC instantiation of the method has a window for
recording rationale with each alternative/criterion evaluation.
5. This methodology gives clear support for three questions decision makers repeatedly ask:
"What is the best alternative?"
"Do we know enough to make a decision yet?"
and " What do we need to do next to feel confident about our decision?"
Future work will focus on combining expert knowledge with task cost and time in order to better
support the third question. In other words, if the cost, time and resource requirement for each
critical alternative/criteria pair was known, then a better cost/benefit evaluation of the sensitivity
could be provided.
7. References
[Akin 86] Akin, O. Psychology of Architectural Design, Pion Limited, England, 1986.
[Blessing, 94] Blessing, L., A Process-Based Approach to Computer-Supported Engineering
Design. Black Bear Press, Ltd. Cambridge, 1994.
[D'Ambrosio 94] D'Ambrosio, Bruce. Local expression languages for probabilistic dependence.
International Journal of Approximate Reasoning. 1994; 11:1-58.
[D'Ambrosio, 95] D'Ambrosio, B. And D.G. Ullman, "Decision Problem Representation for
Collaborative Design. In working Notes of the Workshop on Building Probabilistic Models,
IJCAI 95, Montreal, pp17-22.
[D'Ambrosio 96] D'Ambrosio, B. and Burgess, S. Some experiments with Real-time Decision
Algorithms. Proceedings of the Eleventh Conference on Uncerainty in AI. Portland, OR, Aug,
1996. Morgann Kaufman, Pubs.
[Edwards 77], Edwards, W., Use of Multiattribute Utility Measurement for Social Decision
Making, in Conflicting Objectives in Decisions, edited by Bell, D., Keeney, R.L., and Raiffa, H.,
Wiley 1977, pp 247-266.
[Edwards, 95] Edwards, W. And Barron, F. Smarts and Smarter: Improved Simple Methods for
Multiattribute Utility Measurement. To Appear in Organizational Behavior and Human Decision
Making.
[Herling 95] Herling, D., Engineering Decision Support System (EDSS), ASME DE-Vol 83,
1995 Design Engineering Technical Conferences, Vol 2, pp 619-626.
[Herling 97] Herling, D., Development and Evaluation of a Decision Support System, Thesis for
Oregon State University, 1996.
[McGinnis 92] McGinnis, B., D.G. Ullman, "The Evolution of Commitments in the Design of a
Component," Journal of Mechanical Design, Vol. 144, March 1992, pp. 1-7.
[Rittel, 73] Rittel, H.W.J. and Webber, M.M., Dilemmas in a General Theory of Planning,
Policy Sciences, Volume 4, 1973, pp 155-169.
[Shacter and Fung 90] Shachter, R. and Fung, R.,"Contingent Influence Diagrams", Advanced
Decision Systems Technical Report, September 1990.
[Stauffer 87] Stauffer, L. "An Empirical Study on the Process of Mechanical Design", Doctoral
Dissertation, Department of Mechanical Engineering, Oregon State University, Sept 1987.
[Stauffer 91] Stauffer, L.A., D.G. Ullman, "Fundamental Processes of Mechanical Designers
Based on Empirical Data," Journal of Engineering Design, Vol. 2, No. 2, 1991, pp. 113-126.
[Ullman, 96] Ullman, D. G. The Mechanical Design Process, 2nd ed, McGraw Hill, 1996.
[Ullman 95] Ullman, David G. and Bruce D'Ambrosio, "A Taxonomy for Engineering Decision
Support Systems", International Conference on Engineering Design, ICED95, Praha, Czech
Republic, Sept 95, pp 714-715.
[Yakemovic, 89] Yakemovic, K. and Conklin, J. The Capture of Design Rationale on an
Industrial Development Project: Preliminary Report. Technical Report STP-279-89, MCC, July,
1989.
Return to Table of Contents
1. This research has been supported by the National Science Foundation under grant DDM-
9312996. The opinions in this paper are the authors' and do not reflect the position of the NSF or
Oregon State University.
2. This is formally called stochastic sensitivity analysis with policy recomputation.
3. Note that there are other types of evaluation used during design. See [Ullman 96] and [Herling
97] for details.
4. Contact the authors for availability [ullman@engr.orst.edu or dambrosi@cs.orst.edu].
5. Knowledge about the alternatives and criteria change during problem solution [McGinnis 92]
no matter the level of effort at the beginning to fully define everything. This maturing of the
information crucial to the problem solution is seen as evolutionary.
6. For a complete discussion on how alternatives are compared to criteria and each other see
[Herling 97] or [Ullman 96].
7. Here knowledge is self assessed. It is assumed that all team members are acting for the welfare
of the team and thus their self assessment is assumed sufficiently accurate for methodology. See
the discussion on consensus in Section 4.3.
8. We are considering using W. Edwards SMARTER technique. This only requires acquiring the
rank ordering of the criteria by importance and imposing a logarithm weighting scale on the order
[Edwards, 95].
9. 0 It is more usual, perhaps, to simply represent confidence as a likelihood statement on the knowledge node.
However, we find the explicit graphical representation useful. These can be interpreted as standard belief net nodes
which have been observed.
10. For some criteria the degree to which satisfaction can be achieved can be measured. This
will be the topic of a future paper.
11. Note that this is not an averaging of the team members preferences, clearly a violation of
Arrow's impossibility theorem, but averaging of the results of evaluation on which there is
consensus. This will merely be used as a base point for the next step in the decision process.
12. The use of the average is used because of the team consensus. If there was not consensus or
the results varied wildly, the analysis can be continued using the results from each of team
evaluation results (columns 4-6) in Table 4.
 The paper begins with an example problem,
Section 2. The decision making model described
here has been used to support a number of
industrial problems. One has been simplified here
to provide a thread to the concepts presented in this
paper. In Section 3 we present a description of the
characteristics of multi-attribute problems. These
characteristics lead to a Bayean model of multi-attribute problems in Section 4. This model
supports the first two of the questions posed above:
"What is the best alternative?" and "Do we know
enough to make a decision yet?". Further
development of the example problem will
demonstrate this support. The model is extended in
Section 5 to support the third question, "What do
we need to do next to feel confident about our decision?". This support uses a type of sensitivity
analysis we call "expert knowledge analysis"(2) to suggest future courses of action. This section
develops the most important contribution of this paper. The earlier material is included to set the
stage for this work. Again, the example problem will be used to show the simplicity of this
model and the value of the information developed. The paper will end with a summary and
directions for further work in Section 6. At a minimum, the most original contributions of this
paper can be appreciated by reading Section 2 and the material from Table 4 onward.
The paper begins with an example problem,
Section 2. The decision making model described
here has been used to support a number of
industrial problems. One has been simplified here
to provide a thread to the concepts presented in this
paper. In Section 3 we present a description of the
characteristics of multi-attribute problems. These
characteristics lead to a Bayean model of multi-attribute problems in Section 4. This model
supports the first two of the questions posed above:
"What is the best alternative?" and "Do we know
enough to make a decision yet?". Further
development of the example problem will
demonstrate this support. The model is extended in
Section 5 to support the third question, "What do
we need to do next to feel confident about our decision?". This support uses a type of sensitivity
analysis we call "expert knowledge analysis"(2) to suggest future courses of action. This section
develops the most important contribution of this paper. The earlier material is included to set the
stage for this work. Again, the example problem will be used to show the simplicity of this
model and the value of the information developed. The paper will end with a summary and
directions for further work in Section 6. At a minimum, the most original contributions of this
paper can be appreciated by reading Section 2 and the material from Table 4 onward.

 When a team is making a decision, there may be many
different viewpoints regarding the importance of
criteria, thus the preference model may vary from
member to member. If there are differing viewpoints,
then the preference model is inconsistent. We handle this inconsistency by eliciting the
weighting factors on the criteria from each team member independently. Although there are
many methods for developing weights
When a team is making a decision, there may be many
different viewpoints regarding the importance of
criteria, thus the preference model may vary from
member to member. If there are differing viewpoints,
then the preference model is inconsistent. We handle this inconsistency by eliciting the
weighting factors on the criteria from each team member independently. Although there are
many methods for developing weights

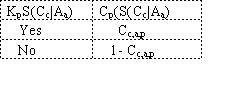
 Our approach to is to aid the team in
planning what to do next is to compute
value of further exploration of each
alternative/criterion pair. This is
accomplished by calculating
EV(Decision | S(Cc|Aa))=yes. This is
found as it was for EV(Decision), but
with a pair of nodes added indicating
perfect knowledge and confidence that
alternative a will satisfy criterion c
(K=1.0, C=1.0). This perfect
knowledge calculation clearly shows the
highest satisfaction achievable if the
knowledge in each of the
alternative/criterion pairs is as high as it
can be. Another way to look at this
calculation is that it is as if a new team
member was added to the team. For
each attribute of each alternative this person is "the" expert and has confidence that the
alternative in question perfectly meets the criterion. This calculation shows how this person
would change the satisfaction and possibly the team's decision.
Our approach to is to aid the team in
planning what to do next is to compute
value of further exploration of each
alternative/criterion pair. This is
accomplished by calculating
EV(Decision | S(Cc|Aa))=yes. This is
found as it was for EV(Decision), but
with a pair of nodes added indicating
perfect knowledge and confidence that
alternative a will satisfy criterion c
(K=1.0, C=1.0). This perfect
knowledge calculation clearly shows the
highest satisfaction achievable if the
knowledge in each of the
alternative/criterion pairs is as high as it
can be. Another way to look at this
calculation is that it is as if a new team
member was added to the team. For
each attribute of each alternative this person is "the" expert and has confidence that the
alternative in question perfectly meets the criterion. This calculation shows how this person
would change the satisfaction and possibly the team's decision.
 The average satisfaction calculation for
the Jackrabbit is now up to .76 while
that for the other two options remains
unchanged. Notice that the .76 < .83
(the perfect knowledge with high
confidence estimate). This is because
the team members were not convinced
they were experts nor that the
alternative fully met the criterion. The
satisfaction results show that the team
as a whole, and each individual, now
has higher satisfaction with the
Jackrabbit than with the elastomer, but
not by much. So, there are now two
candidates and the question, "What do
we do next?"
The average satisfaction calculation for
the Jackrabbit is now up to .76 while
that for the other two options remains
unchanged. Notice that the .76 < .83
(the perfect knowledge with high
confidence estimate). This is because
the team members were not convinced
they were experts nor that the
alternative fully met the criterion. The
satisfaction results show that the team
as a whole, and each individual, now
has higher satisfaction with the
Jackrabbit than with the elastomer, but
not by much. So, there are now two
candidates and the question, "What do
we do next?"
 rationale for each new
record. This data base provides a design
history of the evolution of the information
and the rationale for the decisions made.
rationale for each new
record. This data base provides a design
history of the evolution of the information
and the rationale for the decisions made.