Chapter 17- Hash tables

Associations

We saw earlier a way to get better than O(n) access by assuming the data in our collection was ordered.
Now we will look at a method for relaxing that assumption.
We will also add another wrinkle which is not really fundamental: the maintenance of associations; pairs of values.

An example might be the association of a name with a grade record. A vector is one form of association, maintaining an integer key associated with a value.

But what if the key is not integer (such as a name), or if it is integer but from too large a range (such as a Social Security Number).

The hash table is good when we can afford to allocate a fixed amount of storage to the association
intuition:

A vector is great when the key is a dense set of integers starting from zero. note:
Complexity is constant for add, find, and delete! This is great! but not often key is so conveniently compact
Maybe we can define a mapping from the key to a dense set of integers -how?
What if two keys map to the same integer?

One problem at a time.

Hashing:

A technique for rapid access to members of a collection by value. Three components:

A vector of size n > m=# of members of collection
A hash function which maps a key into an integer in the range 0 - n-1
A collision handling mechanism

Hash Functions:

must accept as input a parameter of type key
must guarantee that output is an integer in range zero to max size-1
For good performance, must distribute kevs over range of vector

Collisions:

when two keys map to the same location we have a collision
collisions can be handled by modifying the storage locations to hold more than one value
for example list, tree, binary search teee
typically a list is used because we expect collisions to be infrequent

Hash Functions

Since we know how to make associations using small integer values (namely, using vectors), one solution is to try to convert a key into an integer value. Such a conversion is called hashing. Almost anything can be used as a hashing function.

Example: Let a = 0, b = 1, c = 2, etc. Select first two letters of name and add together.

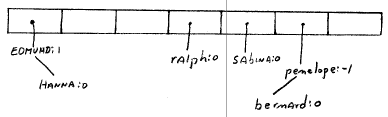
penelope 15 + 4 = 19
sabina 18 + 0 = 18
bernard 1 + 4 = 5
edmund 4 + 3 = 7
ralph 17 + 0 = 17

Perfect Hash Function

A perfect hash function for a set of n elements is a function that transforms each element into a value between 0 and n - 1 with no collisions (two elements having the same value).

For example, set of six names, select third letter and take remainder after dividing by six.

 name value remainder

 Al f red 5 5
 Al e x 4 4
 Al i ce 8 2
 Am y 24 0
 An d y 3 3
 An n e 13 1

Collisions

But what happens in the situation where two entries collide?

 penelope 15 + 4 = 19
 sabina 18 + 0 = 18
 bernard 1 + 4 = 5
 edmund 4 + 3 = 7
 ralph 17 + 0 = 17
 hanna 7 + 0 = 7

Solution - instead of elements, make a vector of collections (called buckets). Elements that collide are then simply maintained in the same collection. Problem of collisions goes away (almost).

 0 {edmund, hanna}
 1 {}
 2 {}
 3 {ralph}
 4 {sabina}
 5 {bernard, penelope}
 6 {}

Class Hash_Table

class TableEntry {
   int key;
   infoType info;
}

class InfoType {
   Object dataField1;
   Object dataField2;
}

class HashTable {
   public final statuc int emptyKey = 0;
   int M;
   int count;
   TableEntry [] T;

   HashTable(int tableSize) {
      M = tableSize;
      count = 0;
      T = new TableEntry[M];
      for (init i = 0; i < M; i++) {
         T[i] = new TableEntry();
         T[i],key = emptyKey;
       }
    }

   void HashInsert(KeyType k, InfoType I) {
      int i;
      int probeDecrement;

      i = h(K);
      probeDecrement = p(K);
      while (T[i].key != emptyKey) {
         i -= probeDecrement;
         if (i < 0) i += M;
      }
      T[i].key = k;
      T[i].info = I;
      count++;
    }

   int hashSearch(KeyType K) {
      int i;
      int probeDecrement;
      KeyType probeKey;

      i = h(K);
      probeDecrement = p(K);
      probeKey = T[i].key;
      while ((K != probeKey) && (probeKey != emptyKey)) {
         i -= probeDecrement;
         if (i < 0) i+=M;
         probeKey = T[i].key;
      }
      if (probeKey == emptyKey) return -1;
      else return i;
   }
}

Note that we don't specify a specific hash function, but that it will have to be included in the class.

Here is one:

public final static int h(String key, int tbaleSize) {
   int hashVal = 0;
   for (int i = 0; i < key.length(); i++) {
      hashVal = 37 * hashVal + key.charAt(i);
   hashVal %= tableSize;
   if (hashVal < 0) hashVal += tableSize;
   return hashVal;
}

There are many variant "open-addressing" schemes for resolving conflicts. Linear probing, double hashing, and a variety of more complex schemes. However, its easier to just keep table size larger than number of entries. Performance can get very bad as tables fill up, but one simple solution is to use "separate chaining".

A generalization of simple chaining is the use of buckets. The idea is simple: each has table entry is itself a collection! What kind? Any kind you like that supports insert, remove, and find. For example, linked list, or better, AVL tree.

Let's look at our initial dataset that way

Asymptotic Analysis of Hash Tables

Major reason for using hash tables is the speed with which operations can be performed. Use as an example the speed of lookup in hash table with m buckets built using trees. Worst case, all elements hash into the same bucket. Can't be any worse than lookup time for AVL Tree - 0(log n).

Best case, elements are uniformly spread over all buckets. Time is 0(log(n/m)).

If the number of buckets is proportional to the number of elements, latter is roughly a constant!

Bucket Sorting

Just as trees, lists, and heaps led naturally to sorting algorithms, hash tables suggest a novel sorting algorithm.

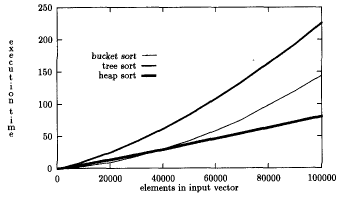
IF we can find a hash function that divides elements so that all values in first bucket are smaller than all elements in second bucket, and all elements in second bucket are smaller than elements in third bucket, and so on - then simply add values into hash table built on top of ordered lists or AVL trees, then pull them out in order. Under the right circumstances can be the fastest of sorting algorithms. Hard part is finding the right hash function. Here is an example. Values selected randomly between 0 and 16000.

Hash function is simply shift left by 4. 1000 buckets.

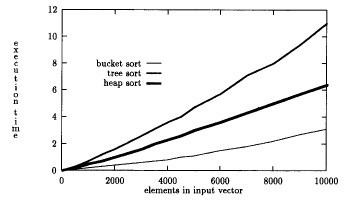
But, as buckets get full, advantage is lost. Why? (Hint - how are we handling collisions?)

Hash Function Techniques

Hash functions can be almost anything. Here are a few of the most common techniques:

Mapping - transform discrete into integer by some algorithm.
Folding - combine two or more integer values together.
Shifting - fast remainder, avoid problems with communitative folding.
Casts - convert memory address into index values.

Often applied in combination with each other.

Mapping

An example of mapping is the transformation a = 0, b = 1, C = 2, etc.

 name value remainder


 Al f red 5 5
 Al e x 4 4
 Al i ce 8 2
 Am y 24 0
 An d y 3 3
 An n e 13 1

Folding

Folding consists of applying a hash function to two or more parts of the key, then combining them together., For example, applying the mapping from the last slide to both the first and second character of a name, then adding the resulting two values. Note that the function applied to the first character need not be the same as the function applied to the second.

 penelope 15 + 4 = 19
 sabina 18 + 0 = 18
 bernard 1 + 4 = 5
 edmund 4 + 3 = 7
 ralph 17 + 0 = 17
 hanna 7 + 0 = 7

Shifting

One common problem with folding is the use of commutative functions. Adam and Daphne both result in the same value, since map(a) + map(d) is the same as map(d) + map(a).

Can mitigate this problem somewhat by shifting the result of the first mapping by some amount before adding the second.

 penelope 15 << 1 + 4 = 34
 sabina 18 << 1 + 0 = 36
 bernard 1 << I + 4 = 6
 edmund 4 << 1 + 3 = 11
 ralph 17 << 1 + 0 = 34
 hanna 7 << 1 + 0 = 14
 adam 0 << 1 + 3 = 3
 daphne 3 << I + 0 = 6

Casts

Casts can convert many types to integer. For example, a cast can convert a pointer to an integer. Useful if two values should have same index if and only if they are exactly the same structure in memory.

When does this happen? "unique" strings is one example: there are packages available which which ensure each distinct string exists only once in memory, so you can test for equality just by testing pointer equality.

Summary

Hash tables: an amazing data structure with constant time random insert, random find.

But note: can't iterate in order over elements. Find next in order is O(n).