Graph Search

Usually when programming we know the specific sequence of steps to execute to obtain a solution. Such a sequence is called an algorithm.

But what if the problem is to find a sequence of steps? For example: find a path through a maze, a route from Portland to Bend, a seqence of steps to turn a pile of parts into a bicycle, ...

A general method for such problems is search.

We will look at two simple forms of search: breadth-first and depth-first search.

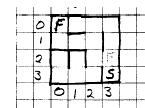
Consider the following maze:

1. Start in 3,3 and can only go up
2. now in 2,3 - can go up, left, pick left.
3. now in 2,2 - up or down - pick down
4. now if 3,2 - only left.
5. now in 3,1 - up or left - pick up.
6. now in 2,1 - dead end! backtrack to 3,1
7. now in 3,1 - this time try left
8. now in 3,0 - only up
9. now in 2,0 - dead end! backtrack to 3,0
10. now in 3,0 - dead end! (tried all alternatives) - backtrack to 3,1
11. now in 3,1 - dead end! backtrack to 3,2
12. now in 3,2 - dead end! backtrack to 2,2
13. now in 2,2 - only up left
14. now in 1,2 - up or left - pick up
15. now in 1,1 - only left
16. now in 1,0 - only up
17. Finish! hooray!

This is called depth-first search. Notice that, like method invocation, we need to be able to access and delete only the most recently added location in the collection of visited locations. Remind you of any data structures we have studied? Which?

What do we need to know about a location? The collection of directions we can go, and the ones we have already tried.

At each step we expand (explore one cell further from) the square most recently added to the collection.

Breadth-first search

Is there another way to find a path through the maze? Yes. This one seems less natural beacuse it jumps around a bit in exploraing the maze.

Maintain a collection of all the squares the program knows how to get to, and expand the oldest square on the collection:

1. 3,3 - add 2, 3 to the collection
2. 2,3 - add 1,3 and 2,2 to the collection
3. 1,3 - add 0,3
4. 2,2 - add 3,2 and 1,2
5. 0,3 - add 0,2
6. 3,2 - add 3,1
7. 1,2 - add 0,2 and 1,1
8. 0,2 - add 0,1 and 1,2
9. 3,1 - add 2,1 and 3,0
10. 0,2 - add 03, and 0.1
11. 1,1 - add 1,0
12. 0,1 - add 0,0 - Finished!

This is breadth-first search. At each step we expand (remove from the collection of squares under exploration, and add all the squares we can reach in one step to the collection) the oldest square in the collection. What data structure does this suggest? If we list the sequence in which squares are explored in depth-first search, we see that the search always moves to adjacent squares:

(3,3); (2,3); (2,2); (3,2); (3,1); (2,1); (3,1); (3,0); (2,0); (3,0); (3,1); (3,2); (2,2); (1,2); (1,1); (1,0)

By constrast, breadth-first search jumps around.

(3,3); (2,3); (1,3); (2,2); (0,3); (3,2); (1,2); (0,2); (3,1); (0,2); (1,1); (0,1)

Another difference: space complexity. How big can a collection grow in depth-first search? Breadth-first?

In depth-first search, the collection size is limited to the solution length - this is easy to see. The elements of the collection at any point in time are simply the steps in the current solution.

In breadth-first search, the collection can be much larger, as large as the branching factor at each choice point raised to the number of choices!.