Trees

We have seen a useful datastructure for managing collections: the linked list. We have also seen an advantage: itr maintains an order over the items, and allows sharing free space among data structures.

But we have also seen a disadvantage: it can only traverse a linked list sequentially. this means random item find is O(n);

Linkedlist carries one pointer per item. If we allowed more pointers could we do better? Well, how does you address book work? If it is like mine, it maintains an index based on first letter. This assumes the items being collected are inherently ORDERED, an assumption we havent made to date. What is complexity? O(n)! Why? EXPECTED case is better WHEN data is nicely distributed.

Still not a complete solution: works ok for nicely distributed names, but what if we don't know anything about the distribution of data to be stored?

A Tree is a more general data structure with provable worst case properties.

A tree is a connected, undirected graph with no cycles.

Better:

A node with no children is a tree. Such a node is called a leaf. A leaf node has a depth of zero
A node with a non-empty collection of disjoint trees is a tree. The trees in the collection are known as the children of the node. The tree so constructed is in turn called the parent to the children.
A node with a non-empty collection is called an interior node, and its depth is one greater than the maximum depth of any child.
There is a single node with no parent, called the root.

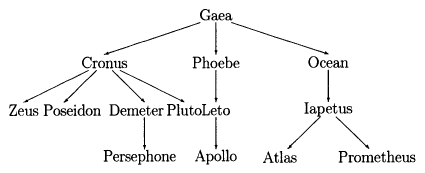
In the above family tree, Gaea is the root. Cronus, Phoebe, and Ocean are here children (or, the roots of the subtrees of the tree rooted at Gaea...)

Trees can be used for many purposes. For example, there are at least two uses for trees in processing expressions in a programming language. Suppose we have the following expression:

if (a < b) max - b; else max = a;

A parse tree shows how the expression can be interpreted as a sentence in some formal grammar. A grammar (one form of one, at least) is a set of rules that can be used to generate the set of legal sentences. For example, given the grammar:

<statement> ::= <select-statement> | <expr>
<select-statement> ::= if(<expr>) <statement> else <statement>
<expr> ::= <relational-expr> | <assign-expr> | identifer
<relational-expr> ::= <expr> < <expr>
assign-expr> ::= <expr> = <expr>

Then we can generate the example expression by selecting the following choices starting from sentence. The fact that we can generate the expression shows that it is a legal element of the language defined by the grammar. The parse tree is an aid in both the generation process and in subsequent interpretation of the expression.

Parse Tree

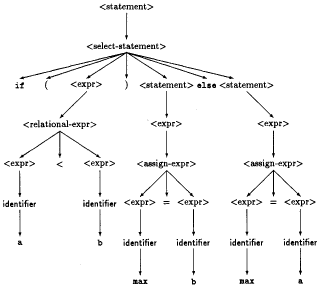
From the parse tree we can generate an expression tree, shown below for our sample expression. Code can be generated directly from a traversal of the expression tree.

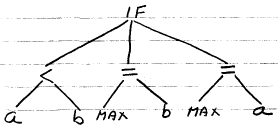
A binary tree is a tree in which each node has at most two children.

Theorem: a full finary tree of height n will have 2^n nodes.

Proof: by induction.

base case: a tree of height 0 has a single node, by definition.
induction step:
- we can make a full binary tree of height n+1 by creating a root and giving it two children of height n
- each child will have 2^n leaves, by the induction hypothesis
- the children are disjoint, by definition
- so total leaves = 2*2^n = 2^(n+1).

Theorem 2: The number of nodes in a full binary tree of height n is 2^(n+1) -1.

So what? So, this can be inverted: The height of a full binary tree holding n nodes is ~ log(n)!

So what - so height grows as the log of the number of elements, so? Remember that the log is a very slow growing function. a full binary tree of height 20 has over 1 billion nodes in it. a full binary tree of height 100 has one node for each atom in the universe!

So what? Now - assume you start at the root, and have a map giving you directions to any node. (ie, left child, right child, stop at the 7-11, ...) the number of edges you have to follow is exactly the height of the tree.

So, if there is a simple way to figure out which way to go at each node, you can reach any node in the tree in log(n) time!

Complete Trees

Well, not often we have exactly a power of two nodes. A complete tree is one in which the difference between the longest and shortest path is 1, and the nodes are filled in left to right.

Complete Tree

A complete tree of height n has at least 2^n nodes.

A complete binary tree containing n nodes must have at least one path of length roundUp(log(n))
In a complete binary tree containing n nodes the longest path is roundUp(log(n))

One more step, then we will switch from graph theory to data structures.

Height Balanced Trees

In a height balanced tree the absolute value of the difference at any node between the longest path in the left and right subtrees is at most one. Over the tree as a whole, differences in paths can be much larger.

Height Balanced Tree

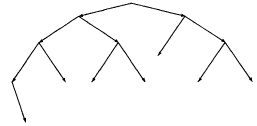
Smallest Number of Nodes in a Height Balanced Tree

An interesting (and useful) question is the smallest number of nodes in a height balanced tree of depth n. If we let Mn represent the function yielding the minumum number of nodes for a height balanced tree of depth n, we obtain:

M(0) = 1
M(1) = 2
M(n+1) = M(n - 1) + M(n) + 1
M(n) ~= 1/SQRT(5) *( (1+SQRT(5))/2)^n - 1
n ~= 1.44 log(M(n))

That is, the longest path is still logarithmic in the number of nodes.

Implementation of Trees

We have two basic collection tricks:

vectors
pointers

Both can be used for binary trees. Let's start with vectors. Remember that we want local operations. That is, as in the count example we saw in chap 11, we want to be able to define all operations in terms of a node and its children and parent. So, we need a vector mapping that enables us to get from a node to its children and back again.

Hmm... well suppose we put the root node in position 0. Ok, then let's put its children in postions 1 and 2. Then if we list the children of 1 and 2 next... The idea is that, since each node has two children, maybe we can figure out where a nodes children are from the location of the node. We can do arithmetic on vector subscript to move around the tree. Here is the mapping:

chidren of node at i are at 2*i+1 and 2*i+2.

Vector encoding of a tree

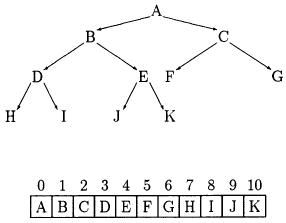
This representation is invertible - that is, we can also find a parent given a child subscript. Just (i-1)/2.

Good idea? Well, the usual problem with vectors: doesn't grow cheaply. One other problem: if it is not a complete tree, can be very storage inefficient:

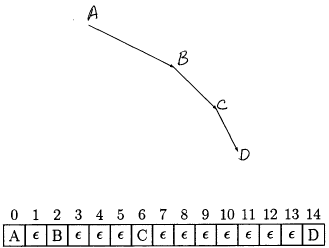
Dynamic Memory (pointer) implementation of Trees

Here is the node class from chapter 12. The idea, remember, is that we will, at each node, keep pointers to the parent node and to each child node. For a binary tree we know exactly how many children there are, so we can allocate a pointer for each. For more general trees we might want to use a list data structure to hold the collection of children. (So, the most primitive "data structure" we have for a collection is simply a set of veraibles, one for each member of the collection!).

class TreeNode {
   ComparisonKey key;
   TreeNode lLink;
   TreeNode rLink;

   TreeNode TreeNode(ComparisonKey x) { key = x;}
}

Well, that's nice. But what is this "ComparisonKey" stuff? "ComparisonKey" is an Interface. From Standish:

public interface ComparisonKey {
   int comparesTo(ComparisonKey value);
}

What the heck is an interface?

public AddressBookEntry implements ComparisonKey {
   String name;
   String street;
   String city;
   String state;
   String zip;

   public int comparesTo(ComparisonKey rhs) {
      return name.comparesTo( ((AddressBookEntry)rhs).name);
   }
}

So the idea is that when we say a class "implements compares", we are promising two items can be compared. Actually, we are promising something stronger - that an instance can be compared with an instance of ANY class that implements compares. However, our methods will break if we actually try this (in the cast), so we have to be sure to never allow this to happen. We defined trees recursively, and I mentioned that most operations on trees are also defined recursively. Let's look at one of the simplest, size:

   int size() {
      return 1+
         ((lLink == null) ? 0 : lLink.size()) 
         +((rLink == 0) ? 0 : rLink.size());
   }

Here is another one, copy:

   TreeNode copy() {
   TreeNode newNode = new TreeNode(info);
   if (lLink) newNode.lLink = lLink.copy();
   if (rLink) rLink = rLink.copy();
   return newnode;

Tree Traversals

Lists and vectors have obvious traversal order. For trees there is no such obvious ordering. Traversals are formed out of different combninations of:

Do somthing at a node
do it at left child
do it at right child.

If we always do left before right, only 3 combinations. To these we will add one other, levelorder. Levelorder is the same order in which nodes would be visited by breadth-first search, starting from the root.

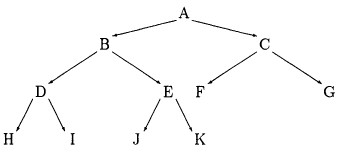
Lets try them on the following tree:

node, left, right (preorder): + a * 2 + 3 b
left, node, right (inorder): a + 2 * 3 + b
left, right, node (postorder): a 2 3 b + * +
levelorder: + a * 2 + 3 b

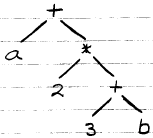
The recursive traversals (the first three) are trivial to write recursively:

   static void preorder(TreeNode current) {
   if (current) {
      System.out.println(key);
      preorder(current.lLink);
      preorder(current.rLink);
   }
}

Why is this static?

Perspective 1: need a base case for recursion
Perspective 2: a pointer can be null!

So the others are pretty similar:

   static void inorder(TreeNode current) {
   if (current) {
      inorder(current.lLink);
      process(current.key);
      inorder(current.rLink);
   }
}
   static void postorder(TreeNode current) {
   if (current) {
      postorder(current.lLink);
      postorder(current.rLink);
      process(current.key);
   }
}

LevelOrder is a bit more complicated, but let's not worry about that for now. There is a problem here. To use this, we have to write a function, process. That's easy. For example, if process is just to print out the value of the node, it is just:

void process(TreeNode current) { System.out.println(current.key); }

But, we have to rewrite the traversers for each "process" function we want to use! (can't give them all the same name!). And besides, the end user can't add methods to our class. One solution is to invoke

current.key.process();

Now the user can provide the methods as part of his/her own class. But still a problem if the user wants to do more than one kind of traversal process. Instead, Weiss provides traversals as iterators.

Let's look at a sample of the postorder iterator:

abstract public class TreeIterator {
   protected BinaryTree t;
   protected TreeNode current;

   public TreeIterator(BinaryTree theTree) {
      t = theTree;
      current = null;
      }
   abstract public void first();
   final public boolean isValid() {
      return current != null;
   }
   final public Object retrieve() {
      if (current == null)
         System.out.println("Not found!");
      return current.element;
   }
   abstract public void advance()
}


public class PostOrder extends TreeIterator {
   protected Stack s;

   public PostOrder(BinaryTree theTree) {
      super(theTree);
      s = new Stack();
      s.push(new STNode(t.root));
   }
   public void first() {
      s.makeEmpty();
      if (t.root != null) 
         s.push(new STNode(t.root));
      advance();
   }
   public advance() {
   if (s.empty()) {
      if (current == null) 
         System.out.println("Postorder advance error");
      current == null;
      return;
   }
   for (; ; ) {
      cNode = s.pop();
      if (++cnod.timesPopped == 3) {
         current = cnode.node;
         return;
      }
      s.push(cnode);
      if (cnode.timesPopped == 1) {
         if (cnode.node.left != null)
            s.push (new StNode(cnode.node.left) );
      }
      else { // cnode.timesPopped == 2
         if (cnode.node.right != null )
            s.push(new STNode (cnode.node.right));
      }
   }

class STNode {
   TreeNode node;
   int timesPopped;

   StNode( TreeNode n) {
      node = n; timesPopped = 0;
   }
   
}

Why do we need a stack for postorder? Let's walk through this for our sample tree.