Recall that the secret of DP is:

divide-n-conquer = single divide into non-overlapping subproblems
DP = divide-n-conquer with multiple divides

In the last section, our examples are all about unary (incremental) divides, but the more exciting divides are binary ones such as mergesort or quicksort best-case. In this section, we will explore the DP instances of such binary-divide recursions.

Number of BSTs

The simpliest example in this category is the number of \(n\)-node BSTs. For example,

n=0: 1 (empty tree)
n=1: 1 (singleton)
n=2: 2 (1->2 or 1<-2)
n=3: 5 (1->2->3, 1->(2<-3), 1<-2->3, 1<-2<-3, (1->2)<-3)

        1        1             2           3          3
         \          \        /   \       /         /
           2           3    1     3     2       1
             \       /                /           \
              3     2                1             2

How to count these numbers \(B(n)\) for an arbitrary \(n\)?

Hint: in the quicksort section, we discussed its connection to BSTs: the recursion tree of quicksort is a BST, with the pivot as the root. Does this give you any idea?

Yes, the difference is that in this problem, the pivot is non-deterministic: it can be anywhere from 1 to \(n\), exactly like our analysis of average-case quicksort. You just need to try all possible partitions. Indeed, that analysis uses DP ideas, although we didn’t elaborate on this connection back then.

For any pivot \(i=1\ldots n\) as the root of BST, we divide this \(n\)-node problem into two subproblems:

• the left subtree has \(i-1\) nodes, so it should have \(B(i-1)\) shapes;
• the right subtree has \(n-i\) nodes, so it should have \(B(n-i)\) shapes.

Combining them, a pivot of \(i\) would result in \(B(i-1) \otimes B(n-i)\) BSTs. Here the combination operator \(\otimes\) is \(\times\) because any BST on the left can be combined with any BST on the right.

That’s the case of one divide. What about the different divides? Yes, summarize them with the new summary operator \(\oplus\)! In our case, \(\oplus\) is clearly \(+\). So:

\[ B(n) = \oplus_{i=1\ldots n} [B(i-1)\otimes B(n-i)]\]

Base case? Only \(B(0)=1\) is needed; everything else including \(B(1)\) can be derived from it using the recurrence.

Time complexity? Obviously \(O(n^2)\).

Note that this problem is not only our first binary-branching DP example, but also the first DP that has multiple (more than two) divides per (sub)problem (\(\oplus_{i=1\ldots n}\)). The three examples in the previous section are all unary branching with two divides per (sub)problem. So this problem greatly expands our view on DP, and is by far a better representative of DP.

Catalan Numbers

This \(B(n)\) series is actually a famous concept in mathematics: the Catalan numbers. There are numerous interpretations of Catalan numbers (besides our number of BSTs), all related to beautiful recursions. Here are just a few of them:

• number of shortest paths in a square grid from the top left corner to the bottom right corner;
• number of bracketings;
• number of polygon triangulations
• number of …

See more on Wikipedia.

Here we want to discuss one interpretation: the number of (balanced) bracketings with \(n\) pairs of parentheses. For example:

n = 0: 1 bracketing
n = 1: 1 bracketing:  ()
n = 2: 2 bracketings: (()) or ()()
n = 3: 5 bracketings: ((())) or (()()) or ()()() or (())() or ()(())

Or equivalently, in terms of mountain plots where / is ( or push stack and \ is ) or pop stack:

n = 1: /\

n = 2: 
       /\
      /  \  /\/\

n = 3:
       /\        
      /  \    /\/\            /\        /\
     /    \  /    \  /\/\/\  /  \/\  /\/  \

Although the 1-1-2-5 sequence matches number of BSTs perfectly, it’s not very obvious to see the connection between the two problems.

Here is a first attempt to solve this problem recursively (and by DP):

Let \(P(n)\) be the number of bracketings with \(n\) pairs of parentheses. We divide this problem into the following two cases depending on whether the leftmost ( and the rightmost ) form a matching pair:

• (****) where the outermost ( and ) match and now the problem is reduced to a smaller subproblem \(P(n-1)\), e.g., to compute P(3), you first compute (P(2));
• the leftmost ( and rightmost ) do not match; so we split these \(n\) pairs into the left \(i\) balanced pairs (\(0<i<n\)) and right \(n-i\) balanced pairs. this means we split into subproblems \(P(i) \times P(n-i)\), e.g., to compute P(3), you decompose into:
  • ++---- where the ++ is P(1) and the ---- is P(2)
  • ----++ where the ---- is P(2) and the ++ is P(1)
  • sum up the results of different split points like in number of BSTs, i.e., \(\sum_{0<i<n} P(i) \times P(n-i)\)

However, you quickly realize this scheme overcounts:

\[P(3) = P(2) + [P(1)P(2) + P(2)P(1)] = 2 + [1\cdot 2 + 2\cdot 1] = 6\]

Why? Because the second case (split) overcounts the ()()() case, which is covered by both ++---- and ----++:

()()()
++----
----++

That’s a big problem! How to fix that?

Well, we need a completely new (and slightly less intuitive) recursion. Instead of asking whether the outermost parentheses match, we now asks the rightmost ): which ( do you match? Or equivalently, how many pairs of parentheses are there between the matching ( and the rightmost ), including themselves? If the answer is \(n\), then the outermost parentheses match. If the answer is 1, then the rightmost () match. In any case, if there are \(i\) \((1\leq i \leq n)\) pairs of parentheses between the rightmost ) and its matching (, then we can divide into two subproblems:

• the \(i-1\) pairs before the matching ( of the rightmost ): \(P(i-1)\);
• the \(n-i\) pairs inside the matching ( and rightmost ): \(P(n-i)\).

Here is a picture of this new decomposition:

*****(^^^^^)
 i-1   n-i

Now we arrive at the exact same equation as the number of BSTs:

\[P(n) = \sum_{1\leq i \leq n} P(i-1) \times P(n-i)\]

Note: This contrast between our first, overcounting, attempt and the the correct solution is very important. In fact, it will show up again in our discussion of RNA folding, a more advanced DP problem, where the first attempt is known as “CKY” and the second one as “Nussinov”.

Question: now can you align the five BSTs for \(n=3\) with the five bracketings?

Extensions

A recursion like this can be easily extended to solve many similar problems, such as

• average work of quicksort (see Sec. 1.2)
• number of level-balanced BSTs (the heights of the subtrees differ by at most 1)
• number of size-balanced BSTs (the sizes of the subtrees differ by at most 1)
• “optimal” BSTs according to some criteria (i.e., the most balanced BST)

Caveat: the average height of BST (also discussed in Sec. 1.2), however, requires a much more complex recursion, because you need the max operator to determine the height based on subtree heights, but those heights are themselves random variables. Only knowing their mean values is not enough to calculate the max between them accurately. You would end up undercounting the height.

Hypergraph Interpretation of Branching DP

We said each DP algorithm has a graph interpretation. But actually, for binary-branching DP, we need to extend the concept of graph to a slightly more general concept called hypergraphs. In a graph, each edge connects one node to another node. This would be enough for unary branching DP, because each node is a subproblem, and one subproblem reduces (in one divide) to a smaller subproblem. However, in binary branching DP, a problem is divided into two or more subproblems (in each divide). Therefore, we need a hyperedge to connect several nodes (subproblems) into one node.

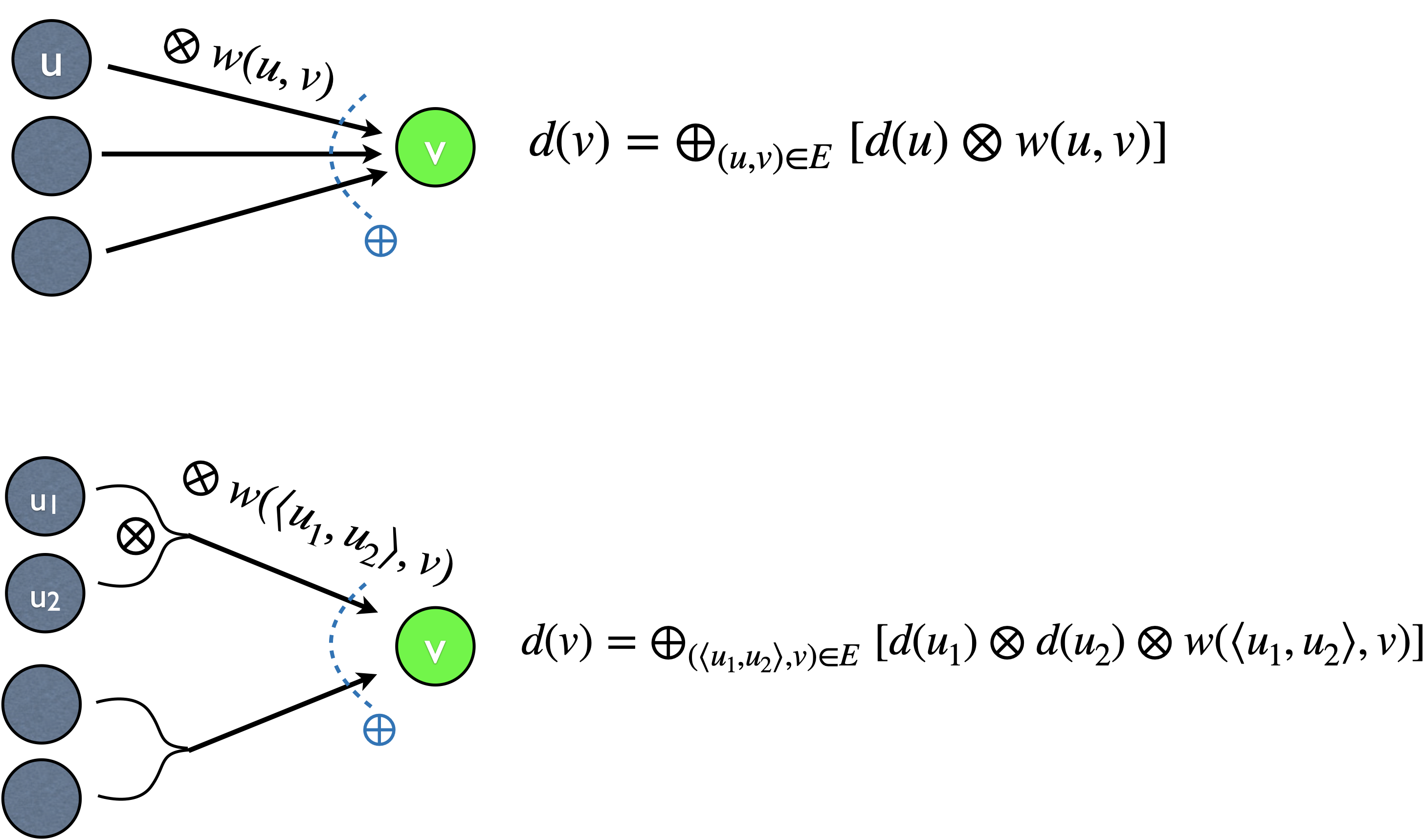
In our BST example, each node \(B(n)\) has \(n\) incoming hyperedges, and each such hyperedge is binary, combining \(B(i-1)\) and \(B(n-i)\) into \(B(n)\). Now you can see that the combination operator \(\otimes\) is naturally associated with each hyperedge, and the summary operator \(\oplus\) is associated with each node. This framework is also equivalent to an AND-OR graph, where each hyperedge is an AND-node and each node is an OR-node.

Also note in the above figure, for completeness, I added edge weigths \(w(u,v)\) and hypereedge weights \(w(\langle u_1, u_2\rangle, v)\). For example, in MIS, the edge weights are \(w(i-2, i)=a[i]\) and \(w(i-1, i)=0\). In the BST example here, the hyperedge weight is 1 (\(\times 1\)).

Most textbooks do not teach the concept of hypergraphs. Instead, they call this type of branching instances “DP over intervals” (such as RNA folding). That interpretation, however, is far too narrow and does not show the real picture. For example, the BST problem here can’t be interpreted as “intervals” because there is no interval here (our \(B(\cdot)\) is a unary function).

In later sections we will see more instances of DP over hypergraphs, which do use intervals \([i,j]\) to define subproblems:

• RNA folding
• context-free parsing
• matrix-chain multiplication
• optimal BST over a list with a distribution
• optimal polygon triangulation

You will see that these seemingly unrelated problems are all equivalent in the hypergraph framework.

I hope my point is clear so far: we should view DP from an abstract point of view, which unifies many different problems in the same framework. The two advanced concepts introduced so far, semiring (with two operators \(\otimes\) and \(\oplus\)) and hypergraph, are the most powerful tools to understand DP in a deep and unifying way.

Historical Notes

The hypergraph view of DP is a classical idea discussed by many authors. See also my tutorial on DP under semiring and hypergraph frameworks.