\(\newcommand{\topk}{{\text{top-}k}}\)
RNA Folding
You might be very familiar with DNA and protein but not very familiar with RNA. Actually, in biology, RNA is even more important than either DNA or protein, because RNA can play both the “informational role” (which DNA plays) and the “functional role” (which protein plays):
| molecule | role | information (idea) | function (real work) |
|---|---|---|---|
| DNA | CEO | only | NO |
| RNA | directors | messenger RNA | non-coding RNA |
| protein | workers | NO | only |
As you can see, DNA (CEO) can only pass information but can’t do real work, while protein is the other way around. RNAs as directors can both pass information and do real work. Therefore, it is widely believed that life started with the versatile RNAs only (the RNA world hypothesis), and later on DNA and protein evolved to specialize in either informational and real work.
RNA is also important because our world has just been turned upside down by an RNA virus SARS-CoV-2 (in fact, most viruses bothering us are RNA viruses, including common cold, flu, HIV, Ebola, Rabies, etc.), and this pandemic was contained partly by messenger RNA (mRNA) vaccines which won the 2023 Nobel Prize.
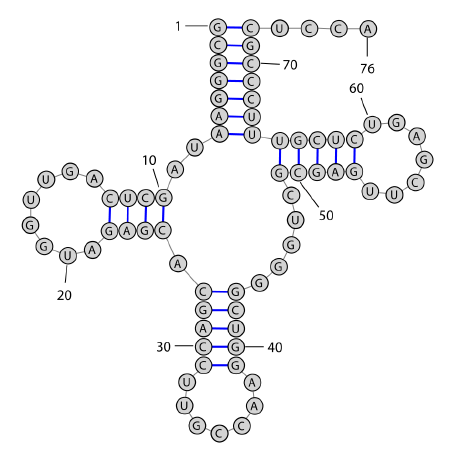
RNAs fold in nature by forming Watson Crick base
pairs (GC, CG, AU,
UA) and Wobble base
pairs (GU, UG), for instance in the
following transfer
RNA (tRNA) structure:

An RNA is a sequence \(x\) where
each \(x_i\) is a nucleotide from the
set {A, C, G, U}, e.g., ACAGU. You want to
predict its secondary structure \(y\)
by tagging each nucleotide as (, ., or
). Here a dot . means this \(x_i\) is unpaired, ( means
this \(x_i\) pairs with some downstream
\(x_j\) and ) means this
\(x_i\) pairs with some upstream \(x_j\). We assume no crossing pairs, so
\(y\) is a balanced dot-bracket string
such as ((.)). Each matching pair must be either a
Watson-Crick pair or a Wobble pair. The following are all valid
structures for ACAGU:
ACAGU
.....
...()
..(.)
.(.).
(...)
((.)) Caveat: in real biology and in the CS textbooks that cover this problem (such as the KT book/slides), there is another “no sharp-turn” constraint which says if \((x_i, x_j)\) forms a pair, then they must be at least three (unpaired) nucleotides between them, i.e., \(j-i>3\), otherwise the “turn” is too sharp. But for simplicity reasons we don’t include this constraint.
Given RNA \(x\), how to find the structure \(y\) for \(x\) with the most number of pairs?
In the example above, ((.)) is the best structure for
ACAGU, with 2 pairs. But for GCACG, the best
is ().(), also with 2 pairs. Other (bigger) examples
(tie-breaking is arbitrary):
GUUAGAGUCU
(.()((.))) # 4 pairs
AUAACCUUAUAGGGCUCUG
.(((..)()()((())))) # 8 pairs
AACCGCUGUGUCAAGCCCAUCCUGCCUUGUU
(((.(..(.((.)((...().))())))))) # 11 pairsActually the RNA folding problem is equivalent to the famous context-free parsing problem (in natural language processing or NLP), and is closely related to the following classical problems:
All these five (5) problems are famous DP instances in hypergraphs rather than graphs. Some textbooks (such as KT) call these problems “DP over intervals” (like spans \((i,j)\)), which is correct, but that’s not getting the essense of the binary-branching nature of these problems.
Now let’s solve it by DP. The subproblem in this DP is the best substructure of a span \((i, j)\) (or equivalently a substring \(x_i ... x_j\)):
\(best(i,j)\) is maximum number of pairs for the substring \(x_i ... x_j\).
Now we can decompose the span \((i, j)\) to even smaller spans, but there are two famous ways in history for this decomposition:
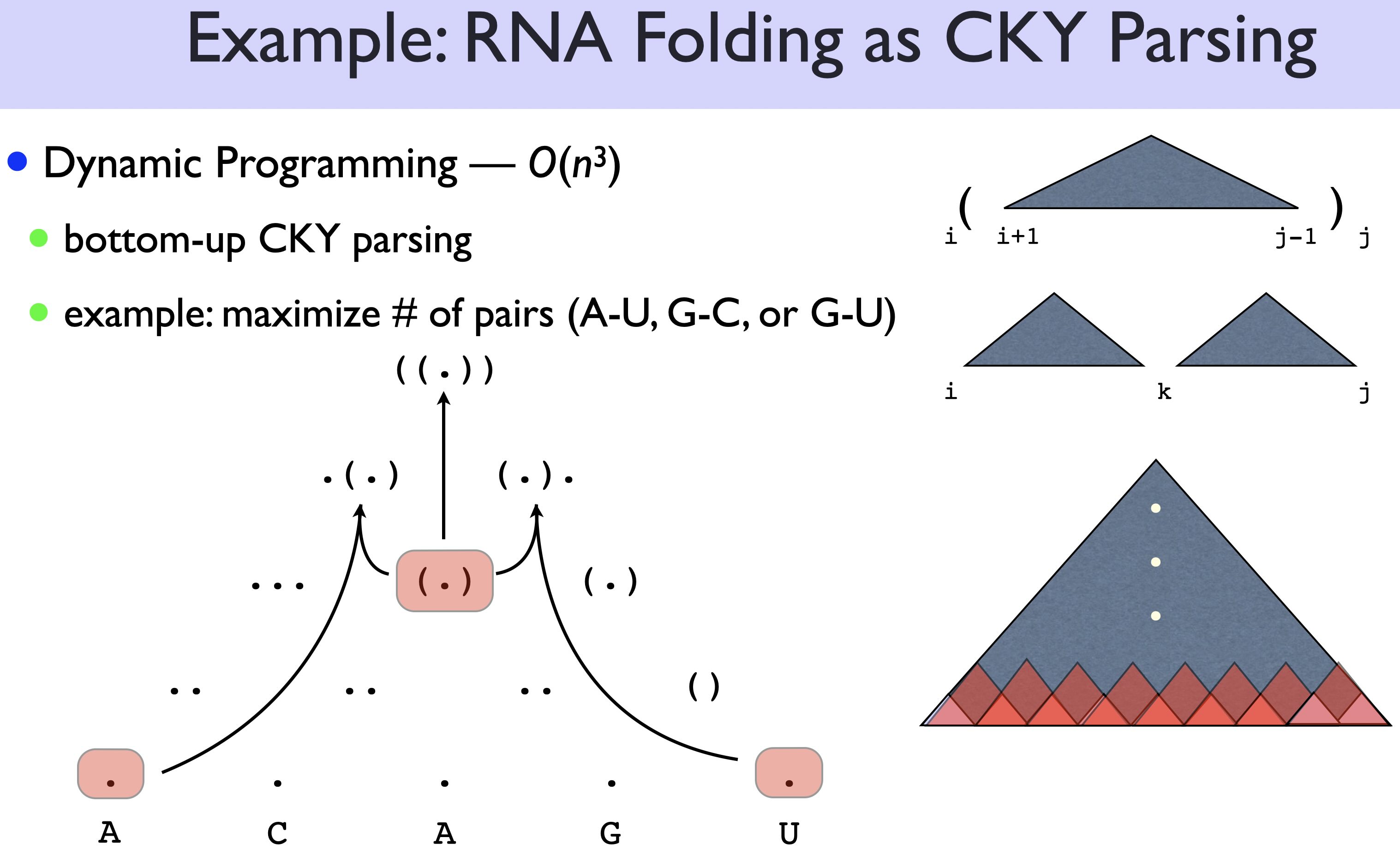
The first way is known as CKY (aka CYK) (~1964) from NLP. There are two cases:
xxxxxxxx = (xxxxxx) | xxxx xxxx
i j i j i k jTherefore:
\[ best(i,j) = \max \begin{cases} best(i+1, j-1) + 1 & \text{$x_i, x_j$ pairable}\\ \displaystyle\max_{i\leq k <j} best(i, k) + best(k+1, j) & \text{(split)} \end{cases} \]
Base cases: \[ \begin{align} best(i, i) &= 0 & \text{singleton spans (length 1)}\\ best(i, i-1) &= 0 & \text{empty spans (length 0)} \end{align} \]
While the first line of base case (singletons) is intuitive, the second line (empty span) seems weird. Is it really necessary? Yes, for example in the \(x_i x_j\) pair clause, if \((i,j)\) is a length 2 span (\(j=i+1\)), then \(best(i+1,j-1)\) is indeed an empty span. This empty span becomes even more useful in the second decomposition (see below).
Interestingly, many years after the NLP field invented the CKY algorithm in the 1960s, the computational biology field independently invented something very similar called the Nussinov algorithm (1978) (important things always get re-invented many times – CKY itself was independently invented by C, K, and Y). But interestingly, Nussinov has a slightly different way of decomposing span \((i,j)\). Instead of doing a case analysis on whether \(x_i\) and \(x_j\) form a base pair, we instead ask whether \(x_j\) is paired:
xxxxxxxx = xxxxxxx. | xxxx(xxx)
i j i j i k jTherefore:
\[ best(i,j) = \max \begin{cases} best(i, j-1) & \text{($x_j$ is unpaired)}\\ \displaystyle\max_{i\leq k <j;\; x_k,x_j \text{pairable}} best(i, k-1) + best(k+1, j-1) +1 & \text{($x_j$ pairs with $x_k$)} \end{cases} \]
Notice that in the second clause, \(k\) can be as small as \(i\), in which case the left subproblem \(best(i, k-1)\) is an empty span (see base cases above); \(k\) can also be as big as \(j-1\), in which case the right subproblem \(best(k+1,j)\) is empty. If \((i,j)\) is a length-2 span that can pair, then both left and right subproblems are empty:
(xxxxxx) # left subproblem empty
i=k j
xxxxxx() # right subproblem empty
i kj
() # both subproblems empty
ijIf you compare these two decomposition schemes, you can find a duality:
Both are \(O(n^2)\) space and \(O(n^3)\) time in the worst case.
Which one is better? Well, either one is good enough for the best
structure problem. CKY is a bit easier to understand and is
aesthetically more pleasing (thanks to symmetry), but Nussinov is a bit
faster since the split point \(k\) is
not arbitrary (e.g., if \(x_j\)=G then only those \(x_k\)=C can match it).
However, we will see below that they make a huge difference in the next two problems.
You can implement either CKY or Nussinov in either top-down or bottom-up style. Which order is easier? Well, as discussed in the DP chapter, top-down can figure out the topological order for you, but bottom-up (nested loops) requires a predefined topological order. What’s a good topological order for this RNA folding problem?
Note that we have three variables: \(i, j, k\). One possibility is to write three nested loops in this order:
for i = 1 to n-1
for j = i+1 to n
for k = i to j-1
...Is this correct? Of course not! These loops traverse spans in this order:
(1,2) (1,3) ... (1,n) <-- this is the whole problem!
(2,3) ... (2,n)
(3,4) ... (3,n)
...
(n-1,n) <-- this is a smallest span!Clearly, the whole problem (1, n) depends on (almost)
all other subproblems and should be the last subproblem to be solved,
but in the above order, it’s attempted way too early. If you use CKY,
and split (1, n) to (1, k) + (k+1, n), but
none of the (k+1, n) spans are ready!
The above order is ridiculous. Instead, you should start from the smallest spans (length 2) and go all the way the largest span (length \(n\), the whole string):
for span = 2 to n
for i = 1 to n-span+1
j = i + span - 1
for k = i to j-1
...The order of spans is now:
(1,2) (2,3) (3,4) ... (n-1,n) -- spans of length 2
(1,3) (2,4) ... (n-2,n) -- spans of length 3
(1,4) ... (n-3,n) -- spans of length 4
... ...
(1,n) -- spans of length nHere is an example for CKY:
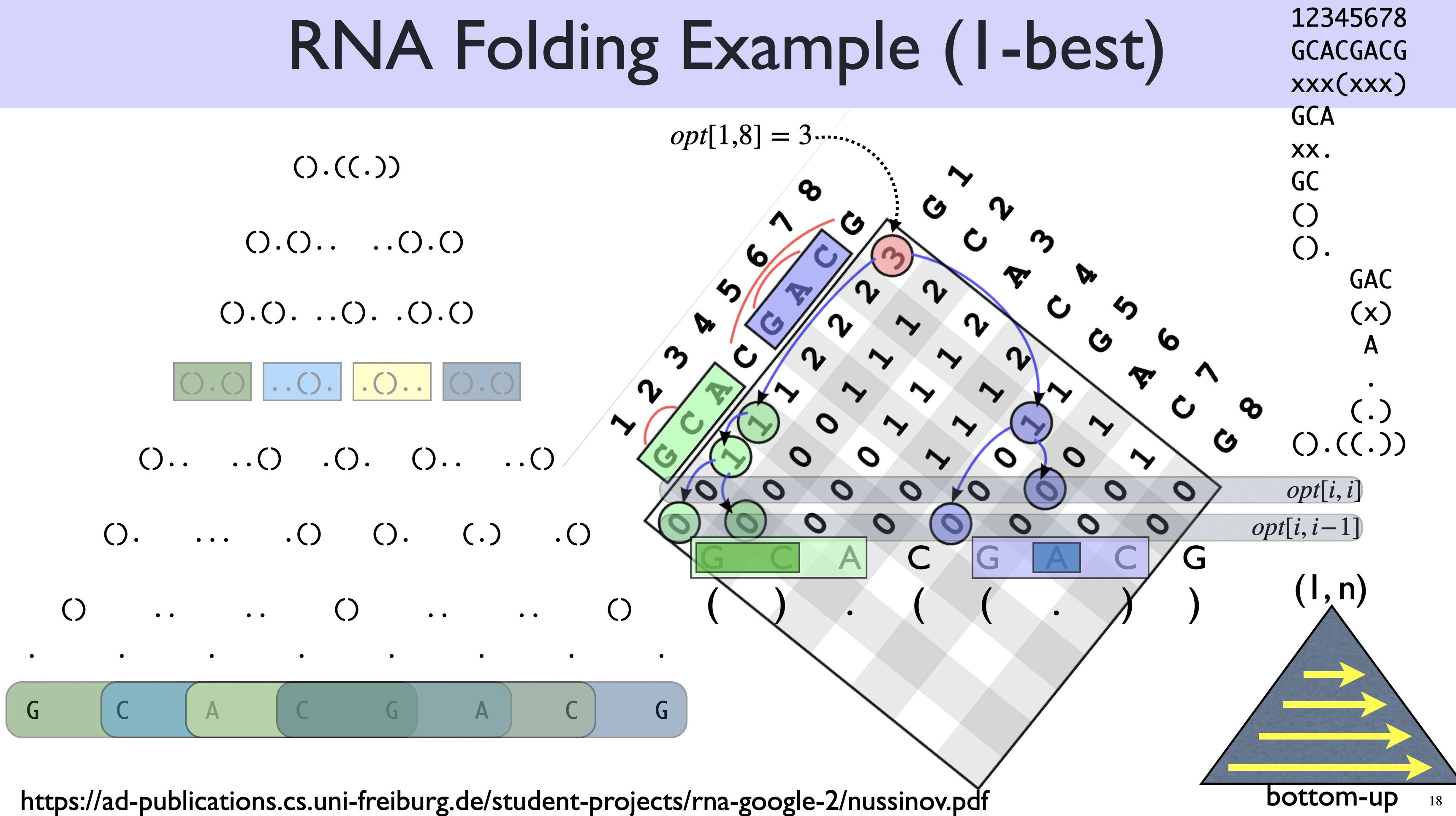
Here is another example for Nussinov, including backtracing for optimal structure:
Now we switch gears to counting the total number of possible
structures for a given sequence. For example, here
total(ACAGU) should return 6:
ACAGU
.....
...()
..(.)
.(.).
(...)
((.)) This problem is very similar to the 1-best structure above, and you can solve it by replacing \(\max\) with \(+\).
But the big question is, can both CKY and Nussinov work for this problem?
Well, CKY doesn’t, due to overcounting. For examples, there are at
least two ways of deriving ()()():
()()() = ()()()
ik j
() = ()
ij
()() = ()()
ik j
() = ()
ij
() = ()
ij
()()() = ()()()
i k j
()() = ()()
ik j
() = ()
ij
() = ()
ij
() = ()
ijBut in Nussinov, there is a unique (and shorter) derivation for this structure (and every structure):
()()() = ()()()
i kj
()() = ()()
i kj
() = ()
kj (i=k) So we write Nussinov equation:
\[ tot(i,j) = + \begin{cases} tot(i, j-1) & \text{($x_j$ is unpaired)}\\ \displaystyle\sum_{i\leq k <j;\; x_k,x_j \text{pairable}} tot(i, k-1) * tot(k+1, j-1) * 1 & \text{($x_j$ pairs with $x_k$)} \end{cases} \]
Note that \(\max\) changes to \(+\), and \(+\) changes to \(*\). Consequently, the base cases would now be 1 (single structure) instead 0.
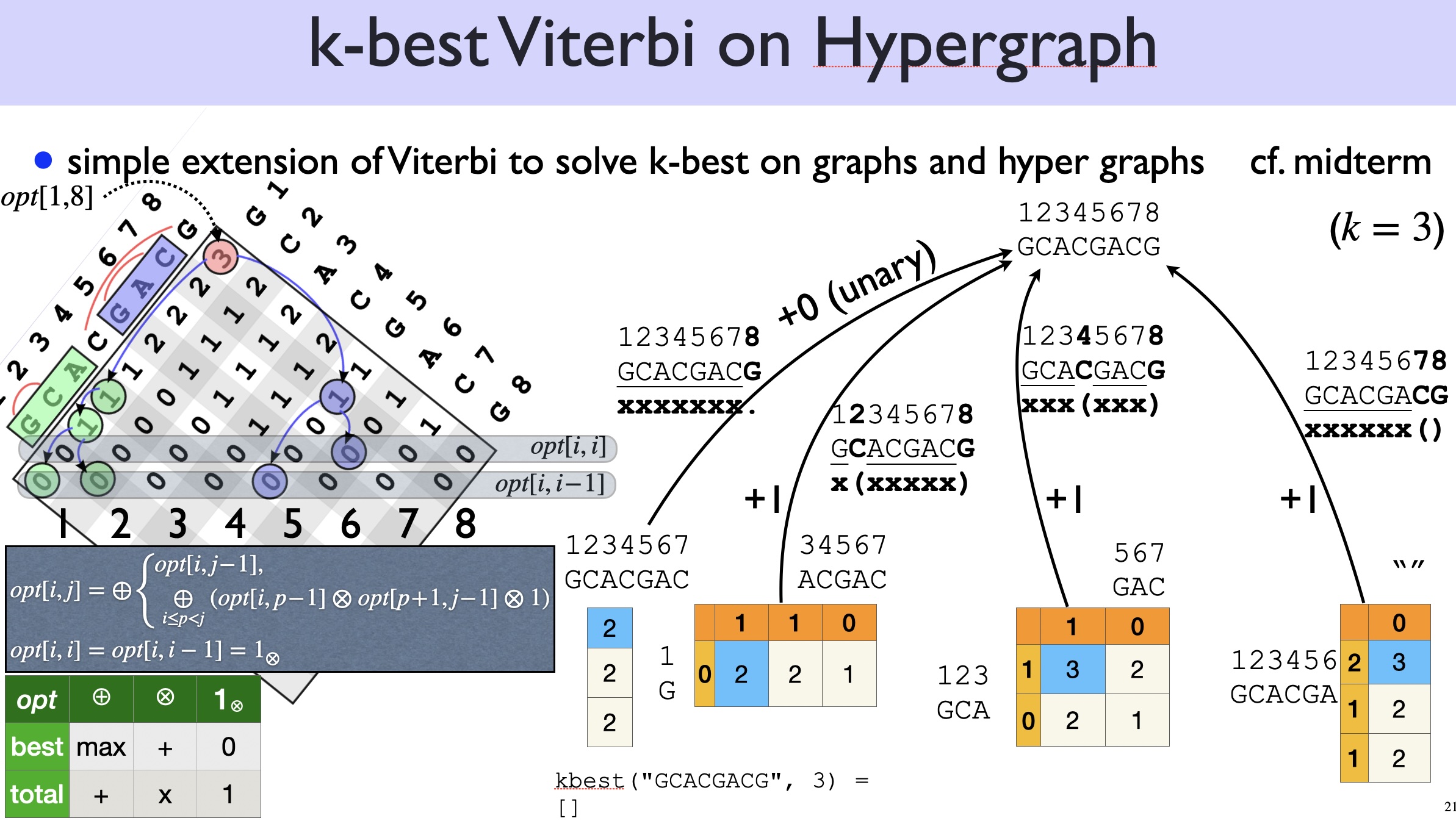
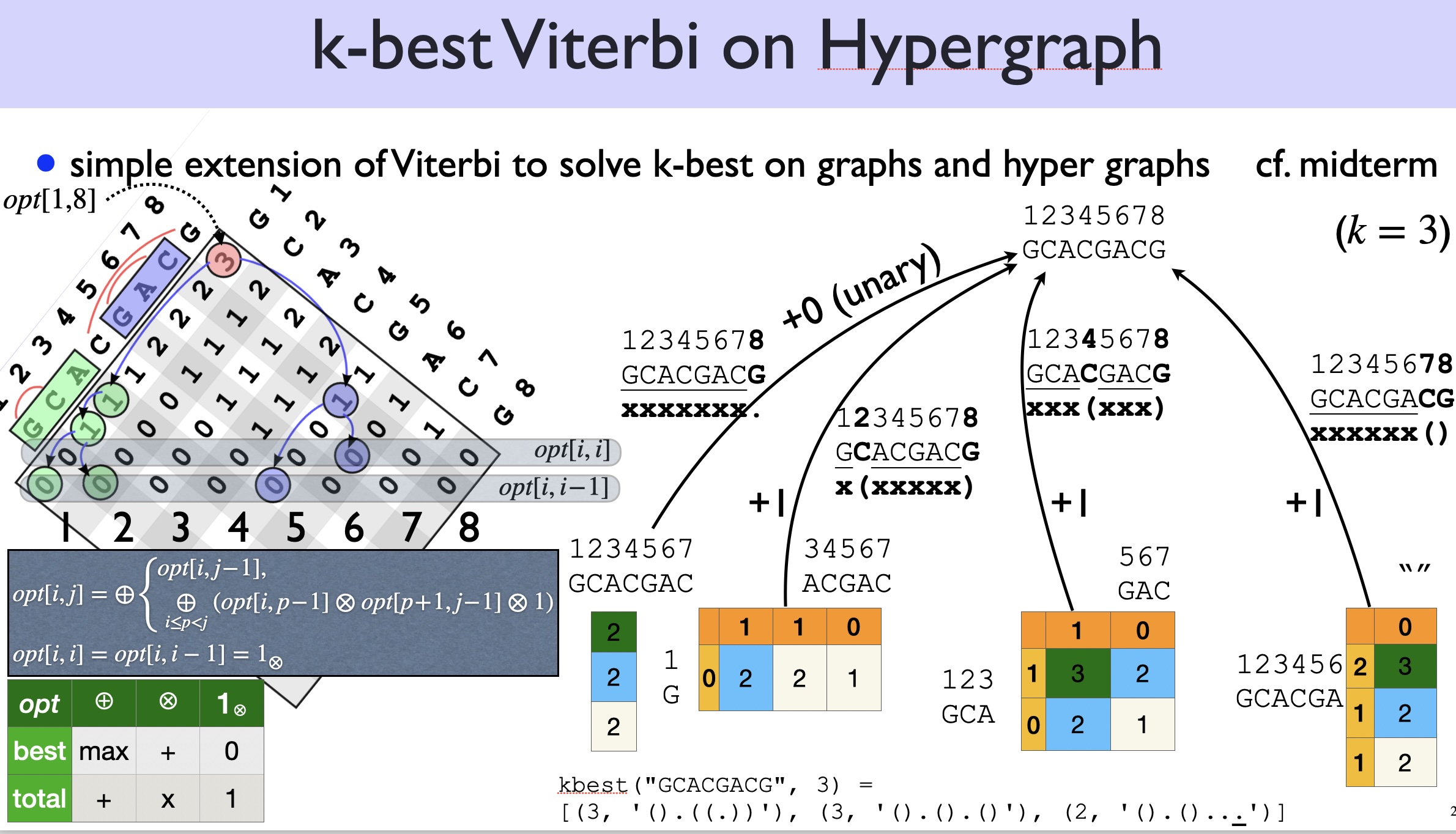
We now want the top-\(k\) structures instead of 1-best, so naturally we should change our subproblem from \(best(i,j)\) to \(kbest(i,j)\):
\(kbest(i,j)\) is the top-\(k\) (sorted) numbers of pairs for span \((i,j)\).
You can use either CKY or Nussinov to solve the \(k\)-best problem, but as discussed above, Nussinov would be easier because there is no overcounting (each structure has a unique derivation). By contrast, if you use CKY, you need to check for duplicates (each structure can be derived multiple times). So below let’s just extend Nussinov from 1-best to \(k\)-best.
First, we need to replace the \(\max\) operator by a \(\topk\) operator:
\[ kbest(i,j) = \topk \begin{cases} kbest(i, j-1) & \text{($x_j$ is unpaired)}\\ \displaystyle\topk_{i\leq p <j;\; x_p,x_j \text{pairable}} kbest(i, p-1) \otimes kbest(p+1, j-1) \otimes 1 & \text{($x_j$ pairs with $x_p$)} \end{cases} \]
Or if we expand the second clause:
\[ kbest(i,j) = \topk \begin{cases} kbest(i, j-1) & \text{($x_j$ is unpaired)}\\ kbest(i, p_1-1) \otimes kbest(p_1+1, j-1) \otimes 1 & \text{($x_j$ pairs with $x_{p_1}$)}\\ kbest(i, p_2-1) \otimes kbest(p_2+1, j-1) \otimes 1 & \text{($x_j$ pairs with $x_{p_2}$)}\\ ...\\ \end{cases} \]
Before we tackle this \(k\)-best RNA folding problem, it’s worthwhile to first study the much simpler \(k\)-best Viterbi problem on directed acyclic graphs (DAGs):

Just like CKY/Nussinov are generalizations of Viterbi from DAGs to DAHs (directed acyclic hypergraphs), now let’s generalize \(k\)-best Viterbi to \(k\)-best Nussinov:
Example: