CS 457/557 -- Winter Quarter 2025

Project #7B

100 Points

Due: March 7

This project is an alternative to the Geometry Shader Project #7A. for those who do not have access to a system that can handle Geometry Shaders.
All others must do the Geometry Shader Project #7A.

You may not use glman for this project.

Twist

This page was last updated: February 11, 2025

Introduction

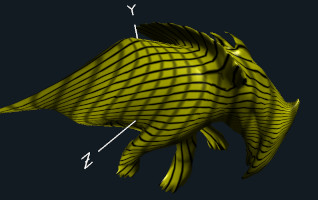
Twisted Twisted about Y

The goal of this project is to twist an OBJ-defined object.

What is twisting anyway? "Twisting" is a rotation about an axis where the angle of rotation is proportional to the distance away from that axis. Half the object is getting a positive twist while the other half is getting a negative twist. (See the video for an example.) Think of twisting a dishrag.

  1. The object needs to have per-fragment lighting. Feel free to hardcode numbers for Ka, Kd, Ks, and Shininess.
  2. The object also needs to have some sort of "hatching" linework applied procedurally in the fragment shader. (The point of the hatching is to make it easier to see the twisting.) It might be best to key off of s or t, but x, y, or z in model coordinates might work too. The hatching only has to be in one direction. (In the images above, I was experimenting with doing it in two directions. You don't have to do that.) You might re-look at the Stripes, Rings, and Dots noteset.

Requirements:

  1. Read in an OBJ file. The choice of object is up to you. Use your LoadObjFile( ) function to read it in. Put it in a display list.

  2. Be sure the OBJ file has surface normals (vn) so that you can light it.

  3. Be sure the OBJ file has texture coordinates (vt) so that you can crosshatch it.

  4. The twisting can occur about the X, Y, or Z axis, you can pick. Different objects look better twisted in different directions. You have rotate functions below for all three directions.

  5. You can implement all 3 directions if you want, but you only have to implement one.

  6. You need to animate the twisting. This can be done with keytiming or by using the Time variable (see below).

  7. The hatching must be stripe-ish. Ellipses do not count as "hatching".

Turn-in:

Use Canvas to turn in your:

  1. Your source files: .cpp, .glib, .vert, .frag
  2. A short PDF report containing:

  3. To see how to turn these files in to Canvas, go to our Project Notes noteset, and go the the slide labeled How to Turn In a Project on Canvas.

  4. Be sure that your video's permissions are set to unlisted.. The best place to set this is on the OSU Media Server.

  5. A good way to test your video's permissions is to ask a friend to try to open the same video link that you are giving us.

  6. The video doesn't have to be made with Kaltura. Any similar tool will do.

Submissions are due at 23:59:59 on the listed due date.

Timing Your Scene Animation

  1. You can use Keytime animation, or,
  2. You can set a constant called something like MS_PER_CYCLE that specifies the number of milliseconds per animation cycle. Then, in your Idle Function, query the number of milliseconds since your program started and turn that into a floating point number between 0. and 1. that indicates how far through the animation cycle you are. So, in Animate( ), you might say: 
    
#define MS_PER_CYCLE	10000
. . .
int ms = glutGet( GLUT_ELAPSED_TIME );
ms %= MS_PER_CYCLE;
Time = (float)ms / (float)MS_PER_CYCLE;		// [0.,1.)

Then, in Display( ), convert whatever you did into an amount of twisting to apply and send that over to your vertex shader as a uniform variable.

Setting up the Object Display List:

In InitGraphics( ): 

glGenLists( 1, &MyObjectList );
glNewList( MyObjectList, GL_COMPILE );
	LoadObjFile( (char *)"dino.obj" );
glEndList( );

In Display( ): 


float twist = ?????;
Pattern.Use( );
Pattern.SetUniformVariable( "uTwist", twist );
glCallList( MyObjectList );
Pattern.UnUse;

How to do the Rotations:

This code goes in the vertex shader: 


vec3
RotateX( vec3 xyz, float radians )
{
	float c = cos(radians);
	float s = sin(radians);
	vec3 newxyz = xyz;
	newxyz.yz = vec2(
		dot( xyz.yz, vec2( c,-s) ),
		dot( xyz.yz, vec2( s, c) )
	);
	return newxyz;
}

vec3
RotateY( vec3 xyz, float radians )
{
	float c = cos(radians);
	float s = sin(radians);
	vec3 newxyz = xyz;
	newxyz.xz =vec2(
		dot( xyz.xz, vec2( c,s) ),
		dot( xyz.xz, vec2(-s,c) )
	);
	return newxyz;
}

vec3
RotateZ( vec3 xyz, float radians )
{
	float c = cos(radians);
	float s = sin(radians);
	vec3 newxyz = xyz;
	newxyz.xy = vec2(
		dot( xyz.xy, vec2( c,-s) ),
		dot( xyz.xy, vec2( s, c) )
	);
	return newxyz;
}

Suggestions for Hatching:

Get ideas from the Stripes, Rings, and Dots noteset. Some of this might help you. (or not...) 


in vec2  vST;
in vec3  vMC;

float
SmoothPulse( float left, float right,   float value, float tol )
{
	float t =	smoothstep( left-tol,  left+tol,  value )  -
			smoothstep( right-tol, right+tol, value );
	return t;
}


// in main( ):
	float numin? = int( ??? / ??? );
	float ?c = numin?*??? + ???/2.;
	float tp = SmoothPulse( ???, ???, ???, ??? );

	vec3 myColor = mix( ???, ???, tp );
	vec3 mySpecularColor = vec3( 1.0, 1.0, 1.0 );
	. . .

Extra Credit (+5 points)

Add a ChromaDepth feature that colors the scene by eye coordinate depth: Red in the front, Blue in the back, and Green in the middle. Include an option which turns the use of ChromaDepth on and off.

I have glasses which will use the ChromaDepth colors to make your scene look really 3D, although you (and we) will know if it is working without having the glasses. Please do not touch the plastic lenses on the glasses. Human fingerprints are nearly impossible to get off them.

uRedDepth and uBlueDepth are meant to be the Z depths in eye coordinates at which the ChromaDepth color interpolation starts and ends. You can make these variable, or you can hardcode them if you find good values for them.

Add some new uniform variables in the fragment shader: 


uniform float	uRedDepth, uBlueDepth;
uniform bool	uUseChromaDepth;

You will need to set those uniform variables: 


	uUseChromaDepth < false >     \
        uBlueDepth <0. 4.4 10.>       \
        uRedDepth  <0. 1. 5.>

Then, in the vertex shader: 


out float	vZ;
. . .
	vZ = -ECposition.z;

Then, in the fragment shader: 


in float                vZ;
. . .
vec3
Rainbow( float t )
{
        t = clamp( t, 0., 1. );         // 0.00 is red, 0.33 is green, 0.67 is blue

        float r = 1.;
        float g = 0.0;
        float b = 1.  -  6. * ( t - (5./6.) );

        if( t <= (5./6.) )
        {
                r = 6. * ( t - (4./6.) );
                g = 0.;
                b = 1.;
        }

        if( t <= (4./6.) )
        {
                r = 0.;
                g = 1.  -  6. * ( t - (3./6.) );
                b = 1.;
        }

        if( t <= (3./6.) )
        {
                r = 0.;
                g = 1.;
                b = 6. * ( t - (2./6.) );
        }

        if( t <= (2./6.) )
        {
                r = 1.  -  6. * ( t - (1./6.) );
                g = 1.;
                b = 0.;
        }

        if( t <= (1./6.) )
        {
                r = 1.;
                g = 6. * t;
        }

        return vec3( r, g, b );
}

. . .

        vec3 myColor = ?????
        vec3 mySpecularColor = vec3( 1.0, 1.0, 1.0 );

        if( uUseChromaDepth )
        {
                float t = (2./3.) * ( abs(vZ) - uRedDepth ) / ( uBlueDepth - uRedDepth );
                t = clamp( t, 0., 2./3. );
                myColor = Rainbow( t );
        }

If you do the ChromaDepth extra credit, you must show us that the red-to-blue color pattern is always in Eye Coordinates. That is, no matter how you rotate the scene, red is always in front and blue is always in back.

If you want to see more ChromaDepth examples, click here.

If you ever want to buy your own ChromaDepth glasses, go here.

Grading:

Item Points
Using an OBJ file 10
Correct per-fragment lighting (we look for the bright spot) 20
Some sort of stripe-ish hatching done procedurally (not a texture, not ellipses) 30
Some sort of twisting of the object 10
Animation of the twisting 30
Extra Credit 5
Potential Total 105