CS 450/550 -- Fall Quarter 2024

Project #6

100 Points

Due: November 27

Shaders

This page was last updated: November 7, 2024

Attention Mac users! Before working on Project #6, please download (right-click) these two files and place them in your project folder: glslprogram.h , glslprogram.cpp If you are a Windows or Linux user, you can use the version of these files you already have or you can use these. Shouldn't matter.

I created a summary document describing the steps in using Shaders. It is called Shader Steps. Check it out. It might help you!

Introduction:

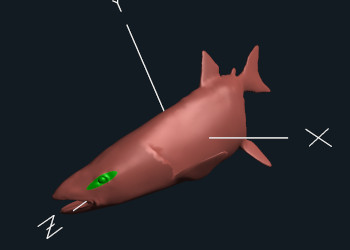
The goal of this project is to use a GLSL vertex shader to animate a swimming salmon and use a GLSL fragment shader to paint the eye. The "swimming" will be animated by using the Time variable and a sine function. The eye will be painted by looking at the salmon's s and t coordinates. The fragment shader will also implement per-fragment lighting.

Learning Objective:

When you are done with this assignment, you will understand how to create a GPU-program, known as a shader. Your vertex shader will let you alter the shape of the object. Your fragment shader will let you control a color pattern on the object. Today's games and movies employ hundreds of shader programs to get the variety of special effects they need. This assignment will also set you up to succeed in CS 457/557, our shaders course which you will be able to take in the Winter Quarter.

Instructions:

  1. The object to draw is a salmon. Here are two OBJ files you can use:
    FileTriangles
    salmon.obj3,270
    salmon_high.obj17,200
    The second one has more triangles in it. I recommend you develop using the first one and then make the video using the second one. You are also free to find your own OBJ file, but it needs to look fish-ish.

  2. Use our GLSLProgram C++ class to create a shader program from the salmon.vert and salmon.frag files.

  3. Write a salmon.vert vertex shader that applies a sine wave to the vertex and passes, to the fragment shader, the vST texture coordinates, the vN normal vector, the vE eye vector, and the vL light vector.

  4. Write a salmon.frag fragment shader that accepts, from the vertex shader, the vST texture coordinates, the vN normal vector, the vE eye vector, and the vL light vector.

  5. To help you get started, here are some program skeletons to work from:

  6. The fragment shader also needs to read in, from the uniform variables, the per-fragment lighting information, uKa, uKd, uKs, and uShininess. The colors can be hard-coded or can be varied. These can all be set once after the shader has been created and left alone after that. InitGraphics( ) is a good place to do this.

  7. If you care, here is what Joe Graphics found is the definition for a color called "salmon":
    const vec3 SALMONCOLOR = vec3( 0.98, 0.50, 0.45 );
    You can use this or any other color you choose. You can pick any color you want for the eye-patch.

  8. In the fragment shader, you will need to experiment to see what are good values for EYES and EYET, the s and t location of one of the salmon's eyes. To give you a hint, EYES needs to be greater than 0.80 and EYET needs to be greater than 0.50.

  9. The first half of the fragment shader needs to look at that fragment's vST texture coordinates and decide if the fragment being worked on right now is over the eye or not. If it is, use the eye color. If it isn't, use the salmon color.

  10. The second half of the fragment shader applies per-fragment lighting to that chosen color.

  11. In your C++ code, use the SetUniformVariable( ) method to set the uniform variables.

  12. Use the in and out keywords to pass 4 variabes from the vertex shader to the fragment shader. Those 4 variables will be interpolated in the rasterizer so that each fragment gets its own copy of them. (On a Mac, use the word varying instead of in and out.)

The GLSLProgram C++ class

The glslprogram.h and glslprogram.cpp files are already in your Sample folder. You just need to un-comment their #include's.

Attention Mac users! Before working on Project #6, please download (right-click) these two files and place them in your project folder: glslprogram.h , glslprogram.cpp If you are a Windows or Linux user, you can use the version of these files you already have or you can use these. Shouldn't matter.

See the class Shader notes for how to use the GLSLProgram C++ class.

Per-Fragment Lighting

You need to do per-fragment lighting. The salmon.vert and salmon.frag programs are already setup for per-fragment lighting.

So, the first half of the fragment shader determines the color to use based on if that fragment is inside the pattern or not. The second half of the fragment shader code uses that color in the per-fragment lighting. The final value assigned to gl_FragColor will be an RGBA that has both the pattern color and the lighting intensity.

Turn-in:

Use Canvas to turn in:

  1. Your .cpp, .vert, and .frag files
  2. A short PDF report containing:

  3. To see how to turn these files in to Canvas, go to our Project Notes noteset, and go the the slide labeled How to Turn In a Project on Canvas.

  4. Be sure that your video's permissions are set to unlisted.. The best place to set this is on the OSU Media Server.

  5. A good way to test your video's permissions is to ask a friend to try to open the same video link that you are giving us.

  6. The video doesn't have to be made with Kaltura. Any similar tool will do.

Grading:

Item Points
Salmon is wriggling/swimming in some way (uniform translation doesn't count) 10
Wriggling/swimming amplitude can be changed 20
Wriggling/swimming speed can be changed 20
Wriggling/swimming frequency can be changed 20
There is a colored patch on one of the eyes 20
Per-fragment lighting works 10
Potential Total 100