CS 453/553 -- Spring Quarter 2019

Project #4: Hyperbolic Geometry

80 Points

Due: April 29

This page was last updated: April 16, 2019

Requirements:

1. Put this project number and your name in the title bar.

2. Using hyperbolic geometry, draw a map of the United States (or something else of your own choosing)

3. Allow the user to interactively translate the map.

4. Use a GLUI spinner or one-handle slider (first argument = false) to change the value of K.
   GLUI_HSlider * KSlider = Glui->add_slider( false, GLUI_HSLIDER_FLOAT, &Kvalue, 0, (GLUI_Update_CB) Sliders );

5. Toggle between polar and Cartesian hyperbolic transformations with a checkbox.

Applying The Hyperbolic Geometry Equations:

For each original Cartesian coordinate pair (x,y):

1. Translate the original x,y by the current translation amount to create a new x',y'.
   Do this by adding the translation values to create a new x.y.
   x' = x + Tx
   y' = y + Ty
   Don't do it with glTranslatef( ).

2. For Hyperbolic-Polar:

   • Compute the x',y' polar coordinate radius, r'.
     r' = sqrt( x'² + y'² )

   • Do not use atan2( ) to get the polar coordinate angle. Instead, get just the cosine and sine of that angle by dividing:
     costheta = x'/r'
     sintheta = y'/r'

   • Perform the hyberbolic transform on the polar coordinate radius to produce r''.
     r'' = r' / (r'+K)

   • Use that cosine and sine to convert from polar coordinates back to Cartesian.
     x'' = r'' * costheta = r'/(r'+K) * (x'/r') = x'/(r'+K)
     y'' = r'' * sintheta = r'/(r'+K) * (y'/r') = y'/(r'+K)

3. For Hyperbolic-Cartesian, use:
   x'' = x' / sqrt( x'*x' + K*K )
   y'' = y' / sqrt( y'*y' + K*K )

4. Then plot that new (x'',y'') point.

Reading and Storing the United States Data

• The state outlines are in a file called proj04.dat. Click here to get it.

• The outlines consist of 68 linestrips. In the file, each linestrip is defined by an integer, N, followed by N X, Y coordinate pairs, then another N, then another N pairs, and so on. The largest N is 263.

• The range of X in the data file is -36.65 to 36.65 and the range of Y is -22.65 to 22.65. The coordinate units of the X, Y pairs is unimportant for this application. They have been converted from latitude-longitude to Universal Transverse Mercator projection to minimize distortion.

• One way to handle this is with a 2D array that is sized for the largest N:

  
  int   Npts[68];
  float X[68][263];
  float Y[68][263];
  
  
  << in InitGraphics( ): >>
  
  FILE *fp = fopen( "proj04.dat", "r" );
  if( fp == NULL )
  {
  	fprintf( stderr, "Cannot open 'proj07.dat' !\n" );
  	exit( 1 );
  }
  
  for( int i = 0; i < 68; i++ )
  {
  	fscanf( fp, "%d", &Npts[i] );
  	for( int j = 0; j < Npts[i]; j++ )
  	{
  		fscanf( fp, "%f %f", &X[i][j], &Y[i][j] );
  	}
  }
  fclose( fp );
  
  
  << In Display( ): >>
  
  for( int i = 0; i < 68; i++ )
  {
  	glBegin( GL_LINE_STRIP );
  	for( int j = 0; j < Npts[i]; j++ )
  	{
  		?????
  		glVertex2f( ??, ?? );
  	}
  	glEnd( );
  }
  
  

• Another way to handle this is with C structures and dynamic memory allocation:

  
  struct xy
  {
  	float x, y;
  };
  
  int        Npts[68];
  struct xy *Outlines[68];
  
  
  << in InitGraphics( ): >>
  
  FILE *fp = fopen( "proj04.dat", "r" );
  if( fp == NULL )
  {
          fprintf( stderr, "Cannot open 'proj07.dat' !\n" );
          exit( 1 );
  }
  
  for( int i = 0; i < 68; i++ )
  {
  	fscanf( fp, "%d", &Npts[i] );
  	Outlines[i] = (struct xy *) malloc( Npts[i] * sizeof(struct xy) );
  
  	for( int j = 0; j < Npts[i]; j++ )
  	{
  		fscanf( fp, "%f %f", &Outlines[i][j].x, &Outlines[i][j].y );
  	}
  }
  
  
  << In Display( ): >>
  
  for( int i = 0; i < 68; i++ )
  {
  	glBegin( GL_LINE_STRIP );
  	for( int j = 0; j < Npts[i]; j++ )
  	{
  		?????
  		glVertex2f( ??, ?? );
  	}
  	glEnd( );
  }
  
  

• Another way to handle this is with a C++ class, dynamic memory allocation, and a Display( ) method for that class:

  
  struct xy
  {
  	float x, y;
  };
  
  class Linestrip
  {
    public:
  	int npts;		// # of points in the line strip
  	struct xy *pts;		// array of point structures
  
  	// constructor:
  
  	Linestrip( int n = 100 )
  	{
  		npts = n;
  		pts = new struct xy[n];
  	}
  
  
  	// method to display the linestrip:
  
  	void
  	Display( )
  	{
  		glBegin( GL_LINE_STRIP );
  		for( int i = 0; i < npts; i++ )
  		{
  			?????
  			glVertex2f( ??, ?? );
  		}
  		glEnd( );
  	}
  
  };
  
  	. . .
  
  Linestrip  *Outlines[68];	// 68 linestrips in usa map
  
  	. . .
  
  << In InitGraphics( ): >>
  
  FILE *fp = fopen( "proj04.dat", "r" );
  if( fp == NULL )
  {
          fprintf( stderr, "Cannot open 'proj07.dat' !\n" );
          exit( 1 );
  }
  
  for( int i = 0; i < 68; i++ )
  {
  	fscanf( fp, "%d", &npts );
  	Outlines[i] = new Linestrip( npts );
  	for( int j = 0; j < npts; j++ )
  	{
  		fscanf( fp, "%f %f", &Outlines[i]->pts[j].x, &Outlines[i]->pts[j].y );
  	}
  }
  
  
  << In Display( ): >>
  
  	for( int i = 0; i < 68; i++ )
  	{
  		Outlines[i]->Display( );
  	}
  
  
  

Suggestions:

As this is a pure 2D application:

• Use gluOrtho2D( -1., 1., -1., 1. ) to define the viewing area instead of glOrtho( ) or gluPerspective( ).
• Use glVertex2f( ) instead of glVertex3f( ).
• Do not use gluLookAt( ).
• Do not do make any calls to glRotatef( ), glTranslatef( ), or glScalef( )!
• Disable depth buffering at the beginning of Display( ): glDisable( GL_DEPTH );

+5 Points Extra Credit:

Because hyperbolic geometry uses a nonlinear equation, but we are drawing long lines, you get display cracks where there are T-intersections in the model, like this:

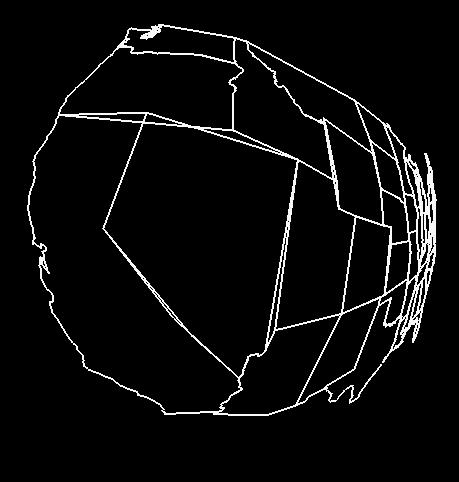
Break each line segment into many line segments so that long straight lines appear curved as shown here:

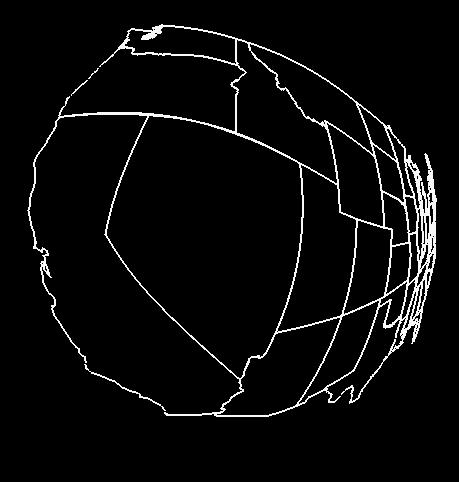
x = (1.-t) * x0  +  t * x1
y = (1.-t) * y0  +  t * y1

0. <= t <= 1.

Grading:

Corvallis: