This page was last updated: February 1, 2023
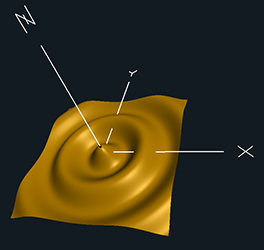
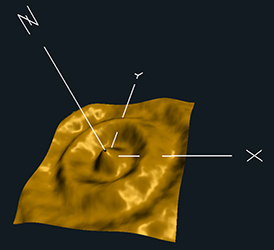
The goals of this project are to use displacement mapping to turn a simple shape into a more interesting one, re-compute its normals, bump-map it, and light it.
The turnin for this project will be all of the source files and a PDF report containing:
This needs to be a PDF file turned into Teach with your other source files. You can use zip to lump your source files together, but be sure to keep your PDF outside your .zip file so I can gather up all the PDF files at once with a script.
As the first part of this is displacing vertices, you need to have enough vertices to displace.
If you are using glman, there is a built-in command to get a quad with a lot of vertices:
QuadXY 0. 1. 128 128
If you are using the API, do something like this:
float xmin = -1.f; // set this to what you want it to be
float xmax = 1.f; // set this to what you want it to be
float ymin = -1.f; // set this to what you want it to be
float ymax = 1.f; // set this to what you want it to be
float dx = xmax - xmin;
float dy = ymax - ymin;
float z = 0.f; // set this to what you want it to be
int numy = 128; // set this to what you want it to be
int numx = 128; // set this to what you want it to be
for( int iy = 0; iy < numy; iy++ )
{
glBegin( GL_QUAD_STRIP );
glNormal3f( 0., 0., 1. );
for( int ix = 0; ix <= numx; ix++ )
{
glTexCoord2f( (float)ix/(float)numx, (float)(iy+0)/(float)numy );
glVertex3f( xmin + dx*(float)ix/(float)numx, ymin + dy*(float)(iy+0)/(float)numy, z );
glTexCoord2f( (float)ix/(float)numx, (float)(iy+1)/(float)numy );
glVertex3f( xmin + dx*(float)ix/(float)numx, ymin + dy*(float)(iy+1)/(float)numy, z );
}
glEnd();
}
It is best if this is placed in a display list, but not absolutely necessary.
This shape is a sine wave that increases as you go down in -Y. If (x,y,z) are the vertex coordinates being processed right now, do something like this in the vertex shader:
z = K * (Y0-y) * sin( 2.*π*x/P )
where K is a constant that controls amplitude of the pleat fold, Y0 is the top of the curtain where there is no z displacement, and P is the period of the sine wave. Y0 can just be a constant set in the vertex shader.
The original x and y, plus the new z become the new vertex that gets multiplied by gl_ModelViewProjectionMatrix.
There is no function to automatically recalculate the normal vectors for the displaced surface. You have to do it yourself. But, in this case, it's not too hard.
Remember that the cross product of two vectors gives you a third vector that is perpendicular to both. So, all you have to do to get the normal is determine 2 vectors that lie on the surface at the point in question and then take take their cross product, and then normalize it.
Because those 2 vectors lie in the plane of the surface, they are tangent vectors. Each tangent is determined by taking calculus derivatives:
float dzdx = K * (Y0-y) * (2.*π/P) * cos( 2.*π*x/P )
float dzdy = -K * sin( 2.*π*x/P )
The tangent vectors are then formed like this:
vec3 Tx = vec3(1., 0., dzdx )
vec3 Ty = vec3(0., 1., dzdy )
The normal is then formed like this:
vec3 normal = normalize( cross( Tx, Ty ) );
Be sure your video shows this to be the correct normal by rotating your object to show that lighting works correctly.
Use per-fragment lighting. Start with the per-fragment lighting shader we looked at in class. Feel free to use it as-is or as a starting point, or feel free to make your own. At a minumim, you must be able to adjust the quantities: Ka, Kd, Ks, shininess, and the light position.
Because we are doing bump-mapping, it must be per-fragment lighting, not per-vertex!
The question marks are not glman-isms -- they are asking you to determine good values in those places.
##OpenGL GLIB Perspective 70 LookAt 0 0 8 0 0 0 0 1 0
Vertex pleats.vert
Fragment pleats.frag
Program Pleats \
uK <? ? ?> \
uP <? ? ?> \
uNoiseAmp <0. 0. ?> \
uNoiseFreq <1. 1. ?> \
uKa <0. 0.1 1.0> \
uKd <0. 0.6 1.0> \
uKs <0. 0.3 1.0> \
uShininess <1. 10. 100.> \
uLightX <-20. 5. 20.> \
uLightY <-20. 10. 20.> \
uLightZ <-20. 20. 20.> \
uColor {1. .7 0. 1.} \
uSpecularColor {1. 1. 1. 1.}
QuadXY -0.2 1. 128 128
Note that you need to break the quad down into many sub-quads (the "128 128" above) so that there are enough vertices to create a smoother displacement function.
You've determined the normal. Now you want to perturb it in a seemingly random, yet coherent, way. Sounds like a job for noise, right?
Use the noise texture capability to get two noise values. These will be treated as an angle to rotate the normal about x and an angle to rotate the normal about y. Allow the variation of two more uniform variables: uNoiseAmp and uNoiseFreq.
vec4 nvx = texture( Noise3, uNoiseFreq*vMC );
float angx = nvx.r + nvx.g + nvx.b + nvx.a - 2.; // -1. to +1.
angx *= uNoiseAmp;
vec4 nvy = texture( Noise3, uNoiseFreq*vec3(vMC.xy,vMC.z+0.5) );
float angy = nvy.r + nvy.g + nvy.b + nvy.a - 2.; // -1. to +1.
angy *= uNoiseAmp;
where vMC are the vec3 model coordinates passed over from the vertex shader.
Rotate the normal like this:
vec3
RotateNormal( float angx, float angy, vec3 n )
{
float cx = cos( angx );
float sx = sin( angx );
float cy = cos( angy );
float sy = sin( angy );
// rotate about x:
float yp = n.y*cx - n.z*sx; // y'
n.z = n.y*sx + n.z*cx; // z'
n.y = yp;
// n.x = n.x;
// rotate about y:
float xp = n.x*cy + n.z*sy; // x'
n.z = -n.x*sy + n.z*cy; // z'
n.x = xp;
// n.y = n.y;
return normalize( n );
}
| Feature | Points |
|---|---|
| Correctly show the effect of changing uK and uP | 30 |
| Correctly show the effects of changing uNoiseAmp | 15 |
| Correctly show the effect of changing uNoiseFreq | 15 |
| Use lighting to show that you have computed the un-bump-mapped normals correctly | 20 |
| Use lighting to show that you have computed the bump-mapped normals correctly | 20 |
| Potential Total | 100 |