This page was last updated: March 31, 2024
This project will use parallelism, not for speeding data-computation, but for programming-convenience. You will create a month-by-month simulation in which each agent of the simulation will execute in its own thread where it just has to look at the state of the world around it and react to it.
You will also get to exercise your creativity by adding an additional "agent" to the simulation, one that impacts the state of the other agents and is impacted by them.
int NowYear; // 2024- 2029 int NowMonth; // 0 - 11 float NowPrecip; // inches of rain per month float NowTemp; // temperature this month float NowHeight; // grain height in inches int NowNumDeer; // number of deer in the current population
const float GRAIN_GROWS_PER_MONTH = 12.0; const float ONE_DEER_EATS_PER_MONTH = 1.0; const float AVG_PRECIP_PER_MONTH = 7.0; // average const float AMP_PRECIP_PER_MONTH = 6.0; // plus or minus const float RANDOM_PRECIP = 2.0; // plus or minus noise const float AVG_TEMP = 60.0; // average const float AMP_TEMP = 20.0; // plus or minus const float RANDOM_TEMP = 10.0; // plus or minus noise const float MIDTEMP = 40.0; const float MIDPRECIP = 10.0;
Units of grain growth are inches.
Units of temperature are degrees Fahrenheit (°F).
Units of precipitation are inches.
omp_set_num_threads( 4 ); // same as # of sections
#pragma omp parallel sections
{
#pragma omp section
{
Deer( );
}
#pragma omp section
{
Grain( );
}
#pragma omp section
{
Watcher( );
}
#pragma omp section
{
MyAgent( ); // your own
}
} // implied barrier -- all functions must return in order
// to allow any of them to get past here
float ang = ( 30.*(float)NowMonth + 15. ) * ( M_PI / 180. ); // angle of earth around the sun float temp = AVG_TEMP - AMP_TEMP * cos( ang ); NowTemp = temp + Ranf( -RANDOM_TEMP, RANDOM_TEMP ); float precip = AVG_PRECIP_PER_MONTH + AMP_PRECIP_PER_MONTH * sin( ang ); NowPrecip = precip + Ranf( -RANDOM_PRECIP, RANDOM_PRECIP ); if( NowPrecip < 0. ) NowPrecip = 0.;
To keep this simple, a year consists of 12 months of 30 days each. The first day of winter is considered to be January 1. As you can see, the temperature and precipitation follow cosine and sine wave patterns with some randomness added.
// starting date and time: NowMonth = 0; NowYear = 2024; // starting state (feel free to change this if you want): NowNumDeer = 2; NowHeight = 5.;
As shown here, you will spawn three threads (four, when you add your own agent):
The GrainGrowth and Deer threads will each compute the next grain height and the next number of deer based on the current set of global state variables. They will compute these into local, temporary, variables. They both then will hit the DoneComputing barrier.
At that point, both of those threads are done computing using the current set of global state variables. Each thread should then copy the local variable into the global version. All 3 threads will then hit the DoneAssigning barrier.
At this point, the Watcher thread will print the current set of global state variables, increment the month count, and then use the new month to compute the new Temperature and Precipitation. Note that the GrainGrowth and Deer threads can't proceed because there is a chance they would re-compute the global state variables before they are done being printed. All 3 threads will then hit the DonePrinting barrier.
After spawning the threads, the main program should wait for the parallel sections to finish.
Each thread should return when the year hits 2030 (giving us 6 years, or 72 months, of simulation).
Remember that this description is for the core part of the project, before you add your own agent to the simulation. That will involve another thread and some additional interaction among the global state variables.
The Carrying Capacity of the deer is the number of inches of height of the grain. If the number of deer exceeds this value at the end of a month, decrease the number of deer by one. If the number of deer is less than this value at the end of a month, increase the number of deer by one.
Each month you will need to figure out how much the grain grows. If conditions are good, it will grow by GRAIN_GROWS_PER_MONTH. If conditions are not good, it won't.
You know how good conditions are by seeing how close you are to an ideal
temperature (°F) and precipitation (inches).
Do this by computing a Temperature Factor and a Precipitation Factor like this:
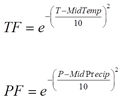
Note that there is a standard math function, exp( x ), to compute e-to-the-x:
float tempFactor = exp( -SQR( ( NowTemp - MIDTEMP ) / 10. ) ); float precipFactor = exp( -SQR( ( NowPrecip - MIDPRECIP ) / 10. ) );
I like squaring things with another function:
float
SQR( float x )
{
return x*x;
}
You then use tempFactor and precipFactor like this:
float nextHeight = NowHeight; nextHeight += tempFactor * precipFactor * GRAIN_GROWS_PER_MONTH; nextHeight -= (float)NowNumDeer * ONE_DEER_EATS_PER_MONTH;Be sure to clamp nextHeight against zero, that is:
Something like this will work for the number of deer:
int nextNumDeer = NowNumDeer;
int carryingCapacity = (int)( NowHeight );
if( nextNumDeer < carryingCapacity )
nextNumDeer++;
else
if( nextNumDeer > carryingCapacity )
nextNumDeer--;
if( nextNumDeer < 0 )
nextNumDeer = 0;
Each simulation quantity will have a structure that looks like this:
while( NowYear < 2030 )
{
// compute a temporary next-value for this quantity
// based on the current state of the simulation:
. . .
// DoneComputing barrier:
WaitBarrier( );
. . .
// DoneAssigning barrier:
WaitBarrier( );
. . .
// DonePrinting barrier:
WaitBarrier( );
. . .
}
The OpenMP specifications says: "All threads in a team must execute the barrier region." This means that placing corresponding barriers in the different functions (like we are doing) is not an option.
So, instead of using the
#pragma omp barrier
line, use this instead:
WaitBarrier( );
You must call InitBarrier( n ) as part of your main program setup process, where n is the number of threads you will be waiting for at the barrier. Presumably this is 3 before you add your own quantity and is 4 after you add your own quantity.
This code seems to work. To make the barriers happen, first declare the following global variables:
omp_lock_t Lock; volatile int NumInThreadTeam; volatile int NumAtBarrier; volatile int NumGone;
Here are the function prototypes:
void InitBarrier( int ); void WaitBarrier( );
In your main program:
omp_set_num_threads( 3 ); // or 4 InitBarrier( 3 ); // or 4
Here is the function code:
// specify how many threads will be in the barrier:
// (also init's the Lock)
void
InitBarrier( int n )
{
NumInThreadTeam = n;
NumAtBarrier = 0;
omp_init_lock( &Lock );
}
// have the calling thread wait here until all the other threads catch up:
void
WaitBarrier( )
{
omp_set_lock( &Lock );
{
NumAtBarrier++;
if( NumAtBarrier == NumInThreadTeam )
{
NumGone = 0;
NumAtBarrier = 0;
// let all other threads get back to what they were doing
// before this one unlocks, knowing that they might immediately
// call WaitBarrier( ) again:
while( NumGone != NumInThreadTeam-1 );
omp_unset_lock( &Lock );
return;
}
}
omp_unset_lock( &Lock );
while( NumAtBarrier != 0 ); // this waits for the nth thread to arrive
#pragma omp atomic
NumGone++; // this flags how many threads have returned
}
How you generate the randomness is up to you. But, feel free to use the Ranf( ) function that you saw in Project #1.
Turn in your code and your PDF writeup into Teach. Be sure your PDF is a file all by itself, that is, not part of any zip file. Your writeup will consist of:
cm = inches * 2.54
°C = (5./9.)*(°F-32)
This will make your heights have larger numbers and your temperatures have smaller numbers.
| Feature | Points |
|---|---|
| Simulate grain growth and deer population | 20 |
| Simulate your own quantity | 20 |
| Table of Results | 10 |
| Graph of Results (one graph only) | 20 |
| Commentary | 30 |
| Potential Total | 100 |