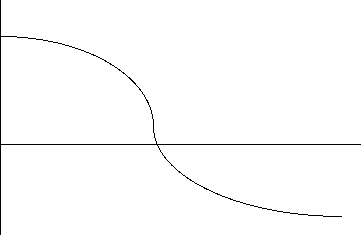
Consider an arbitrary function f(x) that crosses the x axis (f(x)= 0 at some point). Suppose an interval [a,b] is specified such that f(a) f(b) <0.

At each iteration the interval is reduced by comparing the function at points in the interval. The fujnction is evaluated at the midpoint of the interval of uncertainty, and its value (<0, >0, or =0) detrermined.

If f(x_midpoint)= 0, then terminate the process.

If f(x_midpoint)> 0 or <0, then throw out the appropriate endpoint.

Example:

Advantages of the Bisection method

1. Bisection can be shown to be an "optimal" algorithm for functions that change sigh in [a,b] in that it produces the smallest interval of uncertainty in a given # of iterations
2. f(x) need not be continuous on [a,b]
3. convergence is guarenteed (linearly)

    

   Disadvantages of the Bisection Method

    

4. Two initial guesses are required,with f(a) f(b) <0. This may prove difficult
5. If there are multiple zeros in the interval there is no guidance as to which will be chosen
6. Linear convergence may be slow compared to other methods

Golden Section Method

The golden section method will find a minimum, maximum or zero. Two interior points are needed.

No matter how the interval is reduced, one of the old interior points will be in the correct interior position with respect to the new interval.

This ratio r is called the "golden section." This is the ratio of the height to the length of one side of the base for the Great Pyramid. This is also the ratio of the distance from the top of the head to the navel divided by the distance from the navel to the ground of the "optimum" human body, per the ancient Greeks and DaVinci.

Advantages of the golden section method

1. Will find the minimum, maximum or zero of a function
2. The function need not be continuous in [a,b]
3. Convergence is guarenteed. The method will handle poorly conditioned problems.

Disadvantages

1. Convergence is linear
2. Slower than bisection
3. Two initial guesses are required
4. When multiple zeros or optima exist, no guidance as to which will be chosen.

Newtons Method

The function is explicitly used to determine the evaluation point at the next iteration. f(x) is approximated by a line tangent to the function at the last iteration point:

The new point x_k+1 is defined as the zero of the tangent line of f(x) at x_k:

Solving for x_k+1:

The new point x_k+1 denotes the newton approximation to the zero of f(x).

There are, of course, limits on f'(x).

Newtons method does not provide an interval of uncertianty. A new estimate is calculated at each iteration.

Example:

we know the exact solution: x*= b^1/2

using Newtons method: f'(x) = 2x

As an example, given b= 9, find the square root. Use x₀= 1 as a starting point.

x₀=

x₁=

x₂=

x₃=

x₄=

x₅=

Newtons method gives superlinear convergence, but it may work only locally. Convergence can only be guarenteed in a local region except for funtions that are linear or quadratic. This local region may be quite small if the function is highly non-linear.

Example:

Advantages of Newtons method:

1. Superlinear convergence

Disadvantages:

1. may not always work

Polynomial Approximation

We can approximate the function f(x) by a polynomial function:

~f(x)= ax + b (linear approximation)

~f(x)= (1/2)ax² + bx + c (quadratic approximation)

Let's take a look at the quadratic approximation. If a does not equal 0, then ~f has a zero at

What values of a, b, and c to use? We have three unknowns, so we need three equations. One method would be to evaluate f(x) at three points. Another option is to evaluate f(x), f'(x), and f''(x) at one point, and use a quadratic Taylor series approximation:

expanding:

and we can set :

a= f''( x_k)

b= -f''( x_k) x_k + f'( x_k)

c= f( x_k) - f'( x_k) x_k + (1/2)f''( x_k)( x_k)²