General Form

minimize f(x)

(n variables in x)

subject to h(x)=0 (m equality constraints)

g(x) <= 0 (p inequality constraints)

 

Monotonicity analysis can be useful in determining the constraints that comprise the optimal active constraint set. If we know the optimal active constraints set, we can use the Courant heuristic in which we ignore the inequality constraints not in the active set and treat the active constraints as equalities. We are left with an optimization problem subject to equality constraints and can use the Lagrangian technique previously discussed.

What is the activity of some of the inequality constraints cannot be determined? Several approaches will be discussed.

Kurush Kuhn Tucker Conditions

Historical Perspective

• Interest in optimization algorithms in the U.S. was stimulated by the needs of the military for large scale planning and resource allocation during and after World War II. The interest was further stimulated by the introduction of large scale electronic computing in the 1950's.
• The Simplex linear programming method was developed and introduced in the fall of 1947 by George Danzig, who was working for the US Air Force.
• Communications between Danzig and Koopmans at the University of Chicago, and other noted economists led to te extensive application of linear programming to classic economic theory and game theory.
• One early researcher in game theory and digital computers was John von Neumann. von Neumann provided the seed of an idea from duality in game theory to Tucker at Pricton, and one of his grad students, Kuhn. The result of their work was the Kuhn-Tucker conditions for optimality for constrained optimization that was presented at a symposium at UC Berkeley in 1950.
• In the 1980's, it was discovered that W. Karush looked at inequality constraints in his masters thesis at the University of Chicago in 1939, using calculus of variations. This work was not published in the open literature, but is now recognized to be an earier and independent derivation of the Kuhn-Tucker optimality conditions.

Vanderplaats, published in 1984, calles them the Kuhn-Tucker conditions. Papalambros and Wilde, published in 1988, refers to the KKT conditions.

The Lagragian:

First order conditions:

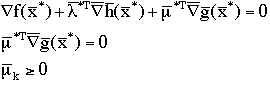
The last two equations are known as the complementary slackness conditions.

Example

min f(x)= 2x₁²+2x₁x₂+ x₂² -10x₁-10x₂

subject to x₁²+ x₂² <= 5

3x₁+ x₂ <= 6

The Lagrangian:

First order conditions:

There are no obvious monotonicities. Assume the constraints are inactive.

Assume constraint 1 is active, constraint 2 still inactive.