GEO599/CS519 Ecosystem Informatics Winter 2005 Assignment 2

In this assignment, you will learn how to apply BUGS to perform some simple data analysis of data on human heights.

Obtaining WinBUGS

Please execute the following steps:
  1. Download and install WinBUGS from the BUGS website.

  2. Download the 2005 WinBUGS license key. Examine this file in a text editor and follow the instructions therein for loading the key into WinBUGS.

Running the Fully Observed Example

Now we will use WinBUGS to repeat (and improve upon) the example that I did in class where we compared the height of men and women in the case where we observe both the sex and the height of each data point.

  1. In WinBUGS, open Help > Doodle Help and consult it while you create a model for the sex-height data analysis problem. The model is shown in the image below:

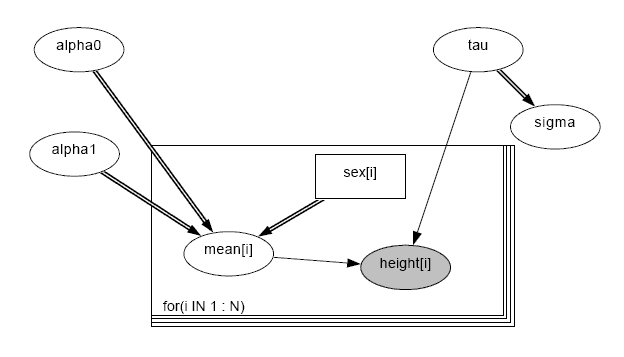
    Each node can be one of three kinds: stochastic (a random variable), logical (computed deterministically via an algebraic formula), and constant (specified in the data file). In this model, sex[i] should be constant, mean[i] and sigma should be logical, and all of the other nodes should be stochastic. You change the node type by click on the type field at the upper left part of the Doodle window.

    When you change mean[i] to be logical, you should then enter its formula into the field named value:.

    Unlike in the model I presented in class, you should use an exponential prior to ensure that alpha1 is positive and define mean[i] using the formula mean[i] ~ alpha0 - alpha1*sex[i]. As you create the model, you should ensure that all of the parameters of each distribution are defined. The only exception is that you should leave the lower bound and upper bound parameters blank in all of the distributions. When your model is finished, click on Doodle > Write Code. This will open a window with the textual version of your model. Delete the semicolon at the end of the first line in this file. I will call this textual window the Text Model Window.

  2. Download the data file from here. Here is a brief explanation of the notation.

  3. Click on Model > Specification... to open the Specification Tool.

  4. Double click on the word "model" at the start of the Text Model Window. Then click on the "Check Model" button in the Specification Tool. The words "model is syntactically correct" should appear in the lower left edge of the main WinBUGS window.

  5. Now click on Open and open the data file. If WinBUGS asks what kind of file it is, choose "text". Click on the word "list" at the start of the data file window. Then click on the "Load Data" button in the Specification Tool. The words "data loaded" should appear in the lower left edge of the main WinBUGS window.

  6. Now edit the "num of chains" box in the Specification Tool to have the value 2. Then click on the "Compile" button.

  7. Click on File > New to create a new empty window. In this window, type a "list" command to define initial values for alpha0, alpha1, and tau. Type a second "list" command to define a second set of initial values for these variables. Now double click on the first "list", move to the Specification Tool and click on the "Load Inits" button. Notice that the small box labeled "for chain" has the value 1, and that it automatically increments to 2 when the initial values are loaded. The words "chain initialized but other chain(s) contain uninitialized values" should appear in the lower left edge of the main WinBUGS window.

    Now double click on the second "list" expression that you wrote, and then click on the "Load Inits" button in the Specification Tool to initialize the second chain. The words "model is initialized" should appear in the lower left edge.

  8. Now we must tell WinBUGS what data to gather during the Markov chain computation. Click on Inference > Samples... to open the Sample Monitor Tool. Type the text "alpha0" into the "node" field and click the "set" button. Repeat this for the "alpha1" and "tau" nodes. This tells WinBUGS to remember each value of these variables that is generated during the Gibbs sampling.

  9. We are now ready to run the chain. Click on Model > Update... to open the Update Tool. The "updates" box specifies the number of steps to run the Markov chain. The "refresh" box tells how often to refresh any dynamic displays. Leave these unchanged and just click on the "Update" button.

    If all goes well, WinBUGS should rapidly perform the 1000 iterations. However, if you get a run-time error, check to make sure that you have the proper probability densities defined and that the initial values make sense. I made the mistake of making tau a gaussian. This allowed the variance of height[i] to become negative, and that caused an error. Under Help > User Manual, there is a section on Tips and Troubleshooting that provides some advice on how to fix problems. The BUGS web page also has some pointers to other useful information.

  10. Now let's visualize what happened with the Markov chains. Go to the Sample Monitor Tool. The box where you typed in the node names has now become a drop-down menu. Select alpha0 from this menu and click on the "history" button. This will show the values of alpha0 during the execution for both Markov chains. If these values seem to be staying within the same range and that range looks reasonable, this is comforting (but not particularly illuminating). Click on the "quantiles" button, and you will see the 95% prediction interval as a function of time. This hopefully shows the two Markov chains converging toward each other. You should inspect this display for alpha1 and tau to decide when the chains have converged. Suppose you decide that they've converged after 400 iterations. Type 400 into the "beg" box in the Sample Monitor Tool. Now any subsequent displays will ignore the first 399 data points.

  11. The next step is to decide how frequently we can safely sample from this markov chain to obtain approximately independent samples. To do this, select a variable (e.g., alpha0) from the node drop-down menu and click on the "auto cor" button. This displays a bar graph showing the degree of autocorrelation between the sampled value of alpha0 at time t and the sampled values at times t - lag, for lag from 0 to 50. Suppose you decide that there are clear autocorrelations up to lag 10. In that case, type 10 into the "thin" box. This tells WinBUGS to compute its statistics using 1 out of every 10 samples from the the Markov chain. You can click "auto cor" again, and now you should see significant autocorrelations only at lag 0.

    With a convergence at iteration 400 and a thinning of 10, we will have only 60 samples of each variable, so that may not been enough. You can run the Markov chain for another 1000 steps by clicking on the "Update" button in the Update tool. This will give us another 100 samples of each variable, which will give nicer estimates of the posterior distributions.

  12. Finally, click on the "density" button to see the kernel density estimate for each of the 3 nodes (alpha0, alpha1, and tau). Similarly, click on the "stats" button to see the mean, median, and 95% prediction interval for each parameter.

Running the Latent Variable Example

Now we will use WinBUGS to repat the latent variable example that I did in class, where we only observe the height of 50 people but we don't know their sexes.

  1. The only change you will need to make in the model is to make sex[i] a stochastic node with the dbern (Bernoulli) distribution, define a parent node theta to specify the proportion parameter of the Bernoulli distribution, and give theta a dbeta distribution with parameters a=1 and b=1 (for a uniform prior).

  2. For the data file, you should remove the data for the sex variable from the "list".

  3. For the initial values, you will now need to provide initial values for the sex[i] variables and for theta. For usex[i], I recommend tossing a coin (or generating random numbers some way) and setting sex[i] to either 0 or 1 (at random) separately for each i. You can write your initial values as sex=c(0,1,1,0,1,...,).

  4. To monitor the values of the sex variables, it is impractical to use the Sample Monitor Tool. Instead, you should click on Inference > Summary... to open the Summary Monitor Tool. Enter the "sex" variable into the "node" field and click the "set" button. This collects the statistics for sex[i] for each i, but it does not collect the other more detailed information. After you have run the markov chains, you can select "sex" from the "node" drop down menu in the Summary Monitor Tool and then click on "Stats". One trick here is that the data are collected from the start of the simulation, so you can't tell WinBUGS when to start or what value of "thin" to use. To accomplish this, you need to use the Update Tool. First, run the Markov chains until they have converged. Then click "clear" on the Summary Monitor Tool. Then go to the Update Tool and enter an appropriate value for "thin". Now each update iteration will perform "thin" number of actual updates and collect one sample. Hence, if you are sampling every 10th value and you want 200 samples, you should set "updates" to 200, and "thin" to 10. This will actually perform 2000 steps and draw 200 points. Now the Summary Monitor Tool will give you good statistics. This is explained in the Tutorial section of Help > User Manual.

Extending the Latent Variable Example (Optional)

If you have time and are curious, try to figure out how to extend the latent variable model to have more than 2 possible sexes. You should start by defining sex[i] to have a dcat (categorical) distribution. A categorical distribution is a multinomial distribution with K possible outcomes (e.g., rolling a die with 6 possible outcomes). You can see an example of this in the "Eyes" example from Help > Examples Volume II. dcat requires a vector-valued parameter "proportions". This vector of values is provided by a Dirichlet distribution ddirch. The dirichlet distribution is the generalization of the beta distribution to a vector of probabilities that must sum to 1. So P[] ~ ddirch(alpha[]) where alpha = c(1,1,1,1,1,1) would generate a vector of 6 probability values that sum to 1.

The tricky part of having more than 2 sexes is that we can't just use the model mean[i] = alpha0 - alpha1 * sex[i], because we don't expect each sex k to be a constant amount taller than sex k-1. One way to do this is to define a set of constant vectors T1, T2, T3, T4, T5 as follows: 

    list(
    T1 = c(0, 1, 1, 1, 1, 1), 
    T2 = c(0, 0, 1, 1, 1, 1), 
    T3 = c(0, 0, 0, 1, 1, 1), 
    T4 = c(0, 0, 0, 0, 1, 1),
    T5 = c(0, 0, 0, 0, 0, 1))

Now we can write the model as 

   mean[i] = alpha0 + alpha1*T1[sex[i]] + alpha2*T2[sex[i]] +
             alpha3*T3[sex[i]] + alpha4*T4[sex[i]] + alpha5*T5[sex[i]]
In this case, alpha0 is the mean height of sex 1, alpha0+alpha1 is the mean height of sex 2, alpha0+alpha1+alpha2 is the mean height of sex 3, and so on. I'm not convinced this is the best way to do this, because if the Gibbs sampler increases alpha1, this causes all of the remaining sexes to get taller so alpha2 then needs to be decreased to compensate. But it does ensure that each sex is well-defined (i.e., they are defined in increasing height order).

To fit more than 2 sexes, you will need more data. The following file gives height data for all of the 21-25 year olds in the NIH study: height-21-25.txt. You will need to reformat it for WinBUGS.

What to Turn In

For the two height models, you should be able to cut and paste the Bayesian network and the relevant graphs into a Word file and then print it out. I would like to see the following:

Please give Bruce D'Ambrosio a hardcopy printout and email me the Word file. I will be in Washington DC Tues-Wed-Thurs of next week, but I'll look at them during my flight back across the country.

Tom Dietterich.