CS533 --- Written Homework 4 --- Due Friday, December 1, 2000 (10:00am)

Consider the following belief network:

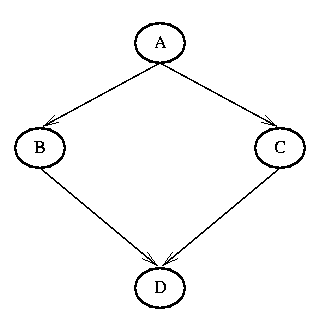The following tables give the conditional probability tables (CPTs) in each node:
P(A)
A=0 A=1
0.4 0.6

P(B|A)
A B=0 B=1
0 1.0 0.0
1 0.5 0.5

P(C|A)
A C=0 C=1
0 0.2 0.8
1 0.3 0.7

P(D|B,C)
B C D=0 D=1
0 0 0.0 1.0
0 1 1.0 0.0
1 0 0.4 0.6
1 1 0.6 0.4

  1. Write an algebraic expression for the joint probability distribution P(A,B,C,D) in terms of the probability distributions stored in each node.

  2. Fill in the following table for the joint probability distribution.

    C=0 C=1
    D=0 D=1 D=0 D=1
    A=0 B=0 ???? ???? ???? ????
    B=1 ???? ???? ???? ????
    A=1 B=0 ???? ???? ???? ????
    B=1 ???????? ???? ????

  3. Write an algebraic expression for the probability distribution P(D) in terms of the probability distributions stored in each node.

  4. Compute the numerical value of P(D=0).

  5. Write an algebraic expression for the probability distribution P(B|D) in terms of the probability distributions stored in each node.

  6. Compute the numerical value of P(B=0|D=0).