Thomas G. Dietterich
Department of Computer Science
Oregon State University
Corvallis, Oregon 97331
Draft of June 24, 1997 .
Fundamental research in machine learning is inherently empirical, because the performance of machine learning algorithms is determined by how well their underlying assumptions match the structure of the world. Hence, no amount of mathematical analysis can determine whether a machine learning algorithm will work well. Experimental studies are required.
To understand this point, consider the well-studied problem of
supervised learning from examples. This problem is usually stated as
follows. An example 
is an n-tuple drawn from some set
X according to some fixed, unknown probability distribution D.
An unknown function f is applied to each example to produce a
label 
. The labels may be either
real-valued quantities (in which case the problem is referred to as a
regression problem) or discrete symbols (in which case the problem is
referred to as a classification problem).
The goal of machine learning algorithms is to construct an
approximation h to the unknown function f such that with high
probability, a new example 
drawn according to D will be
labeled correctly: h(x) = f(x).
For example, consider the problem of diagnosing heart disease. The examples consist of features describing the patient, such as age, sex, whether the patient smokes, blood pressure, results of various laboratory tests, and so forth. The label indicates whether the patient was diagnosed with heart disease. The task of the learning algorithm is to learn a decision-making procedure that will make correct diagnoses for future patients.
Learning algorithms work by searching some space of hypotheses, H, for the hypothesis h that is ``best'' in some sense. Two fundamental questions of machine learning research are (a) what are good hypothesis spaces to search and (b) what definitions of ``best'' should be used? For example, a very popular hypothesis space H is the space of decision trees and the definition of ``best'' is the hypothesis that minimizes the so-called pessimistic error estimate [Qui93].
It can be proved that if all unknown functions f are equally likely, then all learning algorithms will have identical performance, regardless of which hypothesis space H they search and which definition of ``best'' they employ [Wol96, Sch94]. These so-called ``no free lunch'' theorems follow from the simple observation that the only information a learning algorithm has is the training examples. And the training examples do not provide any information about the labels of new points x that are different from the examples. Hence, without any other source of information, there is no mathematical basis for making predictions about f(x).
Hence, the effectiveness of machine learning algorithms in practice depends on whether the hypothesis space H is sufficiently small and contains good approximations to the unknown function f. (The hypothesis space must be small in order to be searched in a feasible amount of time and in order to support statistical judgements of hypothesis quality based on realistic amounts of training data.)
Fundamental research in machine learning therefore involves proposing various hypothesis spaces H and optimization criteria, implementing these proposals as programs, and testing their performance on a large collection of real-world data sets. A large and growing collection of learning problems is maintained at the University of California at Irvine [MM96], and it has been used as the basis for hundreds of experimental studies.
Figure 1 shows a summary of one such study. In this study, the widely used C4.5 decision tree algorithm was compared with a new algorithm, called ADABOOST, developed by Freund and Schapire [FS96]. Both algorithms were applied to 27 different learning problems. For each learning problem, there is a fixed amount of data available in the Irvine collection. To evaluate a learning algorithm, one of two methods are used. In the simple holdout method, a randomly-selected subset of the available data is withheld, the learning algorithm is ``trained'' on the remaining data to produce an hypothesis, h, and the accuracy of h is then measured on the withheld data. In the 10-fold cross-validation method, the data is randomly split into 10 equal-sized subsets. The learning algorithm is executed 10 times--each time, it is trained on all but one of the 10 subsets and then evaluated on the remaining subset. The results of these 10 runs are averaged to estimate the error rate of the algorithm.
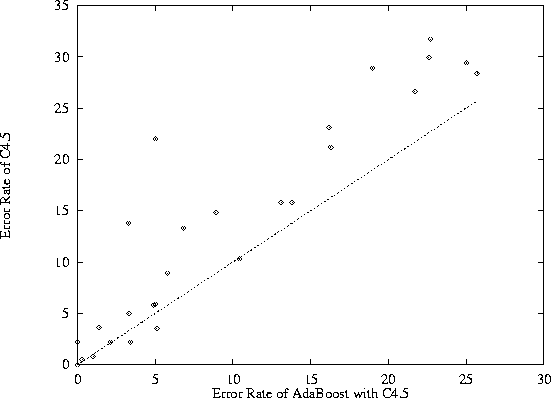
Figure 1: Comparative performance of the C4.5 learning algorithm with
the ADABOOST algorithm applied to C4.5.
Figure 1 is a scatter plot in which each point corresponds to a different learning problem. The x coordinate of each point is the error rate of ADABOOST on that problem, and the y coordinate is the error rate of C4.5. Points that lie above the line y = x have a lower error rate for ADABOOST. The pattern of points reveals that ADABOOST generally performs better than C4.5 on these benchmark problems.
In addition to basic performance comparisons, experimental studies have also been carried out to understand and explain the differences between learning algorithms. The basic strategy is to take two algorithms and consider the effects of modifications to those algorithms that enhance or remove differences between the algorithms. For example, in a comparison of C4.5 and the backpropagation algorithm for training neural networks, Dietterich, Hild, & Bakiri [DHB95] observed that neural networks performed better than C4.5 on the problem of mapping English words into phoneme strings (for speech synthesis). They identified three hypotheses to explain this difference and tested those hypotheses by exploring the effects of changes to C4.5 and backpropagation. For example, a change to both C4.5 and backpropagation to capture certain forms of statistical information eliminated most of the differences between the two algorithms. It did this by improving the accuracy of C4.5 while leaving the accuracy of backpropagation unchanged. Hence, it provides a plausible explanation for why backpropagation was working better--namely, that backpropagation was already capturing this statistical information, but C4.5 was not.
Another experimental strategy involves leaving the algorithms unmodified but altering the training examples to introduce or remove factors believed to be important. For example, to test the noise tolerance of different algorithms, artificial noise can be introduced into training data. Many algorithms make assumptions about the nature of interactions between different features of the input examples. Experiments that systematically manipulate these interactions have demonstrated that some of these assumptions are not as strong has had been assumed. For example, the ``naive'' Bayes algorithm for classification assumes that each feature of the training examples is generated independently of the others given the label f(x). This strong independence is rarely observed in practice, but experimental studies of shown that naive Bayes is very robust to violations of this assumption [DP96].
Given the essential role of empirical research in machine learning, one might assume that mathematical methods have little to offer. However, there has been a strong interplay between theoretical and experimental research in machine learning. The ADABOOST algorithm is a case in point. The algorithm was originally developed based on a theoretical model known as the weak learning model. This model assumes that there exist ``weak'' learning algorithms that can do slightly better than random guessing for some set of hypotheses H regardless of the underlying probability distribution D that is generating the examples. ADABOOST shows how to ``boost'' these weak learning algorithms to achieve arbitrarily high accuracy. While the experimental success of ADABOOST is uncontested, the theoretical explanation for its success in terms of the weak learning model is controversial. Leo Breiman [Bre96] performed a series of experiments calling into question the weak learning explanation and providing an alternative explanation based on an extension of the well-known bias/variance error decomposition in statistics. Schapire, Freund, Bartlett, and Lee [SFBL97] challenged Breiman's explanation with a more refined theoretical account (and associated experiments) based on the maximum margin model first developed by Cortes and Vapnik [CV95]. Breiman [Bre97] has recently responded with a new set of experiments and a new explanation based on a new model, which he calls ``boosting the edge''. This lively interplay between theory and experiment is producing rapid improvements in our understanding of these algorithms and is helping to focus mathematical analysis on the most important fundamental questions as well as suggesting new algorithms of practical importance.
In summary, machine learning is an inherently empirical research area. The fundamental questions in this area require empirical study through the articulation of hypotheses and their experimental investigation. These experiments make use of data sets gathered from real-world applications of machine learning, and there is consequently an important relationship between basic and applied research. However, experimental machine learning research is not applied research--it seeks to answer fundamental questions rather than to produce profitable applications. The success or failure of a particular application effort does not provide insight into fundamental questions--the success or failure is typically unrelated to the quality or appropriateness of the machine learning algorithms. Rather, it is usually determined by the managerial and financial aspects of the project. Furthermore, application projects are designed not to answer fundamental questions but to circumvent them. Progress in fundamental research requires careful design, execution, and interpretation of experiments. Students require training in statistics for experiment design and analysis as well as solid knowledge of the mathematical models developed in computational learning theory.
Our understanding of the fundamental questions in machine learning has been advancing rapidly (along with the quality of the resulting learning algorithms). Much of this progress can be traced to the merging of experimental research (driven by the creation and expansion of the Irvine repository) and theoretical research (initiated by the pioneering work of Vapnik [VC71] and Valiant [Val84]) along with the advances in computer hardware that permit large scale experimentation. Nevertheless, a computational account of the power of people to learn very complex skills, such as vision and language processing, still lies some distance into the future. There are many important fundamental challenges for machine learning research in the decades ahead, and experimental research will be critical to meeting these challenges.
http://www.ics.uci.edu/~mlearn/MLRepository.html, 1996.
Fundamental Experimental Research in Machine Learning
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_navigation -split 0 paper.
The translation was initiated by Tom Dietterich on Tue Jun 24 17:00:06 PDT 1997