Discrete Interval Encoding Tree

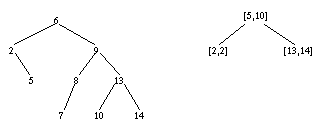
The discrete interval encoding tree is a structure for storing subsets of types having a total order and a predecessor and a successor function.  We consider for simplicity only the case for integer sets; the generalization is not difficult. The discrete interval encoding tree is based on the observation that the set of integers { i| a<=i<=b } can be perfectly represented by the closed interval [ a, b]. The general idea is to represent a set by a binary search tree of integers in which maximal adjacent subsets are each represented by an interval. For instance, inserting the sequence of numbers [6, 9, 2, 13, 8, 14, 10, 7, 5] into a binary search tree, respectively, into an discrete interval encoding tree results in the tree structures shown below:

You can download the implementation in ML or Haskell:

• diet.sml
• diet.hs

A stepwise derivation of an efficient version for the insert function is summarized here.