- Administrativia
- Intro: longest increasing subsequence
- greedy: wrong. O(n)
- brute force: correct. O(2^n). powerset construction
- Big-O informal intro
- quicksort example
- longest increasing subsequence (wikipedia)
- dynamic programming: correct, O(n^2).
- backtracing to print the solution.
- proof of correctness by (complete) induction
- it's possible for O(nlogn) with binary search (beyond this course)
- insertion sort (CLRS 2.3)
- proof of correctness by (simple) induction
- improvements: binary search or linkedlist, but not both
- complexity remains O(n^2) anyways
- review of arrays vs. linkedlists (KT 2.3)
- random
accessinsertion/
deletionfind array O(1) O(n) normal: O(n)
sorted: O(logn)
hashed: ~O(1)linkedlist O(n) O(1) O(n)
- quick sort (CLRS 7.1-2)
- worst-case scenario
- best-case scenario
- connection to binary search trees (CLRS 12.1-2) but not binary search (CLRS 2.3, KT 2.3)
HW1 out (due Mon 1/23). 2 Mon 1/16 Martin-Luther King's Day. no class. - Wed 1/18 - Quiz 1 (20 min.)
- quicksort analysis (CLRS 7.3-4, KT 13.5)
- randomization: shuffling and random pivot
- intuitions why worst-case is rare after randomization
- average-case analysis (expected runtime for randomized quicksort)
(high-level intuitions are important, but details of this proof are not required)
QUIZ 1 3 Mon 1/23 - discussions of Quiz 1
- mergesort (CLRS 2.3, KT 5.1)
- merging two sorted list is linear
- substitution method for analyzing complexity
- on linkedlist
- quicksort vs. mergesort
- why/when quicksort is generally faster? (in place, in memory)
- when is mergesort useful? (linkedlist, files on disk)
- stable sort: mergesort and insertion sort are stable (with careful implemenations)
- quicksort unstable with in-place implementation with randomized pivot
- why stability matters: sorting with multiple keys (last name, first name)
- priority queue / heapsort (CLRS 6)
- complete binary tree, linear (array) representation
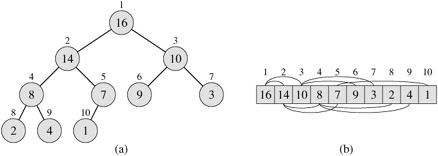
- complete binary tree, linear (array) representation
HW1 due Wed 1/25 - Big-O, Big-Theta, Big-Omega: formal intro (CLRS 3, KT 2.2).
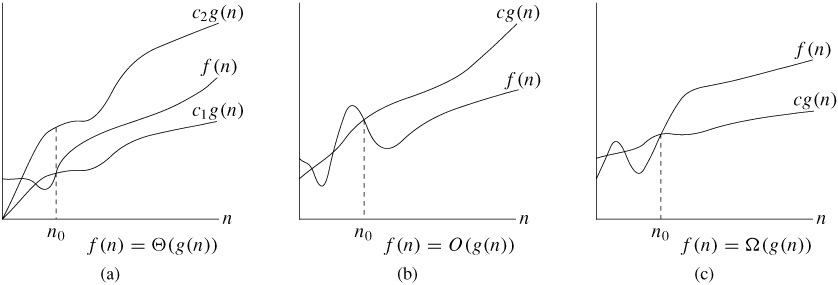
- Substitution and Recursion Tree Methods (brief, CLRS 4.3-4)
- Master theorem (CLRS 4.5), examples:
- T(n) = 2T(n/2) + O(n) (mergesort)
- T(n) = 2T(n/2) + O(1) (binary tree traversal, cf. quiz 1)
- T(n) = T(n/2) + O(1) (binary search)
- T(n) = T(n/2) + O(n) (quickselect)
- heapsort (cont'd)
- priority queue vs. queue: emergency room vs. checkout line
- heap operation: push/insert (add at the end; bubble-up); O(log n)
- heap operation: pop/extract-min (pop root; move the last element to root; bubble-down); O(log n)
- bubble-up and bubble-down are the building-blocks for other heap operations.
HW 2 out 4 Mon 1/30 - heapsort (cont'd)
- use priority queue to model stack and queue (CLRS problem 6.5-7, trivial)
- heap operation: change-key (bubble-up or bubble-down)
- heap operation: build heap (from array)
- method 0: sort it first (overkill!): O(nlogn)
- method 1: insert each element: O(nlogn) (CLRS problem 6-1)
- method 2: heapify (bottom-up or recursive). tight analysis: O(n). (CLRS 6.3)
- formal analyses of methods 1 and 2:
useful fact 1: # of elements with height h is n/2^{h+1}.
useful fact 2: 1/2 + 2/4 + 3/8 + ... = (1/2 + 1/4 + 1/8 + ...) + (0 + 1/4 + 2/8 + 3/16 + ...)
= 1 + (1/4 + 1/8 + 1/16 + ...) + (1/8 + 2/16 + 3/32 + ...) = 1 + 1/2 + ... = 2.
(this derivation of fact 2 is more accessible than the one in the textbook).- method 2: sum O(h) n/(2^{h+1}) = O(n) sum h/2^h = O(n x 2) = O(n).
- method 1: sum O(logn - h) n/(2^{h+1}) = O(nlogn) x sum 1/2^h - O(n) sum h/2^h = O(nlogn) - O(n)=O(nlogn).
- method 2: sum O(h) n/(2^{h+1}) = O(n) sum h/2^h = O(n x 2) = O(n).
- high-level intuitions: method 2 is faster because the majority (lowest levels) requires very little work (bubble-down to the leaves), while method 1 is slow because the majority requires the most work (bubble-up to the root).
- heapsort is O(nlogn): build heap O(n), pop each element O(nlogn).
- example application: k-way mergesort: merging becomes O(k+nlogk)=O(nlogk). (CLRS problem 6.5-9)
Wed 2/1 - review of heapify:
- recursive version: heapify left, heapify right, bubble-down.
T(n)=2T(n/2) + O(logn).
use Master Theorem case 1 (when f(n) small): T(n)=O(n).
this analysis is more intuitive than the sum version in the textbook. - (where as "keep pushing" is T(n)=T(n-1)+O(logn)=O(nlogn).)
- applications: select kth-smallest element: O(n+klogn). fast when k << n.
- recursive version: heapify left, heapify right, bubble-down.
- quickselect (CLRS 9.2, KT 13.5)
- idea from quicksort: partition, but throw half away
- best-case O(n): T(n)=T(n/2) + O(n).
use Master Theorem case 3 (check regularlity!), or geometric series. - worst-case O(n^2): T(n)=T(n-1)+O(n).
- randomized version: expected linear time
- determinstic worst-case linear-time select (CLRS 9.3)
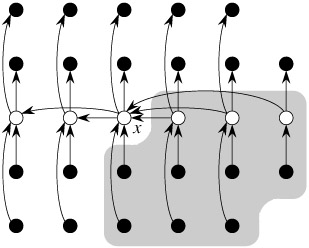
- idea: find a balanced pivot to partition w/o randomization
- 5 steps in each recursive call:
- divide into n/5 groups of 5: O(n)
- insertion-sort each group: O(n)
- recursively find x=median-of-medians: T(n/5).
- partition using x: O(n). at least 3n/10 < x, and at least 3n/10 > x.
- recursion on one half: T(7n/10).
- total: T(n)=T(n/5)+T(7n/10)+O(n).
use substitution method, guess T(n)=O(n), i.e., T(n)<=cn for some c. work out the math. T(n)=O(n). - Why magic number of 5? what about 3, 4, 6, 7? (CLRS problem 9.3-1).
5 is the minimum magic number. e.g., why 4 is not enough:
T(n) = T(n/4) + T(3n/4) + O(n) = O(n^2). - this algorithm is mostly of theoretical interest (constant overhead too large).
5 Mon 2/6 - review of worst-case linear selection
- example applications of selection
- worst-case O(nlogn)-time quicksort based on selection (CLRS problem 9.3-3)
- find k elements closest to median in O(n) time. (CLRS problem 9.3-7)
- find median of two sorted lists in O(logn) time. (CLRS problem 9.3-8)
- lower-bounds for sorting (CLRS 8.1)
decision tree model: each non-leaf node is one comparison, and each leaf node is a complete ordering. the tree should have at least n! leaves: 2^h >= n!, so h >= log n!.
(n/2)^(n/2) <= n! <= n^n, so log n! = \Theta(nlogn). so h = \Omega(nlogn).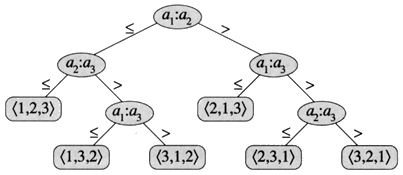
HW2 due Wed 2/8 Topics Covered So Far - Design Paradigms: Divide-and-Conquer
- Analysis Notions: Big-{O, Theta, Omega}, Worst-Case, Best-Case, Average-Case
- Analysis Techniques: Master, Substitution, Recursion Tree
- Data Structures: BST, Heap (Priority Queue), LinkedList
- Algorithms
- Sorting: Insertion, Quicksort, Mergesort, Heapsort
- Selection: Quickselect, Worst-case linear select
- Lower-Bounds: Comparison Sort: O(nlogn)
- heapsort is not stable. example: [3a, 3b, 3c]. pop out: 3a, 3c, 3b.
- O(nlogn)-time to check if there exist x+y=S.
- O(logn)-time to find the number in a (balanced) BST that is closest to query x.
- find the k smallest numbers in a data-stream of n numbers with only O(k) space.
- k-way mergesort. Merging is O(k+nlogk)=O(nlogk).
Overall: T(n)=kT(n/k) + O(n log k). Can't use Master Theorem (why?).
Use substitution instead. Result: O(nlogn). - Pitfalls of using substitution method: must prove the exact form. (CLRS 4.3)
Extra office hour Fri 9:30-11:30, SAL 235. 6 Mon 2/13 MIDTERM 1 (covers all lectures so far). No office hours on Mon/Tue. Wed 2/15 Discussions of Midterm 1 problems. regrade session in office hour. 7 Mon 2/20 PRESIDENT'S DAY -- NO CLASS Wed 2/22 Dynamic Programming - Example Problems
- Review of Longest Increasing Subsequence
- The Unbounded Knapsack Problem (see wikipedia)

- Steps
- Define subproblem
- Recurrence relation
- Reconstructing Optimal Solution
- Implementations
- Bottom-Up
- Top-Down recursive + memoization (e.g. Fibonacci)
- Requirements
- Optimal Substructure (check your subproblem definition)
- Sharing of Subproblems (cf. memoization)
8 Mon 2/27 Dynamic Programming (cont'd) - The 0-1 Knapsack Problem (see wikipedia)
opt[w][i] -- optimal value of a bag of weight w, using items 1..i
- Longest Common Subsequence (Sequence Alignment)
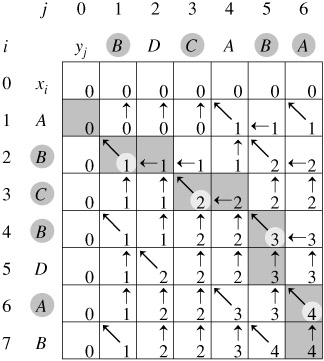
opt[i][j] -- LCS b/w A_{1..i} and B_{1..j}
opt[i][j] = max { opt[i][j-1], opt[i-1][j],
opt[i-1][j-1]+1(A_i==B_j) }applications: sequence alignment (e.g. DNA), edit distance, spelling correction, etc.
- Matrix-Chain Multiplication
Wed 2/29 Dynamic Programming (cont'd) - Matrix-Chain Multiplications
basics: multiplying a p x q matrix with a q x r matrix results in an p x r matrix and takes p x q x r multiplications.
matrix-chain A_1 A_2 ... A_n.
each A_k has dimensions p_{k-1} x p_k (neighboring pairs share one dimension).example: A x B x C
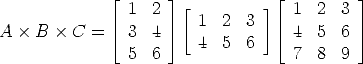
A x (B x C) is better (2x3x3+3x3x2).
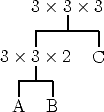 vs.
vs. 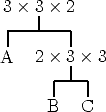
objective: find the order of multiplications that minimizes the total # of scalar multiplications.
m[i, j] -- optimal # of multiplications for subchain A_i x ... x A_j.
m[i, j] = min_{i<=k<j} m[i, k] + m[k+1, j] + p_{i-1} p_k p_j
m[i, i] = 0.
complexity: O(n^3) time, O(n^2) space.
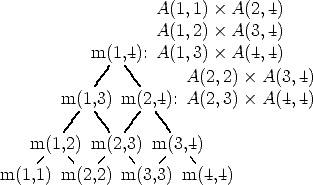
fill in the chart. e.g. A1 : 3 x 2, A2 : 2 x 4, A3 : 4 x 3, A4 : 3 x 2
9 Mon 3/5 Quiz 2 and discussions; DP on graphs and hypergraphs (matrix-chain) Wed 3/7 Viterbi algorithm on DAG; topological sort 10 SPRING BREAK - NO CLASS 11 Mon 3/19 - review on topological sort
- pseudocode: BFS-style
- theorem: the following three are equivalent for directed graph G
- G is acyclic
- G has a valid topological ordering
- the BFS-style topological sort succeeds
- BFS
- connected components for undirected graphs
- strongly-connected components (SCCs) for directed graphs
Wed 3/21 tree traversal review:
[DFS] pre-order, post-order, and (for binary trees only) in-order,
[BFS] level-order.DFS on directed graphs;
DFS edge classification: tree, back, forward, cross.
DFS for undirected graphs: tree and back edges only.12 Mon 3/26 DFS time intervals (easier to understand than edge classification);
DFS for SCCs: Kosaraju's Algorithm (two DFS's, CLRS 22.5);
SCC-DAGWed 3/28 DFS for SCCs: Tarjan's Algorithm (single DFS, see wikipedia).
All topological orders for Matrix-Chain Multiplication DP.
Viterbi algorithm for shortest, longest, and # of paths on DAG.
13 Mon 4/2 MIDTERM 2 Wed 4/4 discussions of midterm 2; discussion of HW4; regrading session.
- review on topological sort