Introduction to Object Oriented Programming, 3rd Ed

Timothy A. Budd

Chapter 6

A Case Study : Eight Queens

Outline

1. Statement of the Problem
2. OOP Approach
3. Observations
4. Pointers
5. CRC Card for Queen
6. CRC Card for Queen - Backside
7. Initialization
8. Finding First Solution
9. Advancing to Next Position
10. Printing Solution
11. Can Attack
12. The Last Queen
13. Chapter Summary

Source Code

• Eight Queens program in C++
• Eight Queens program in Object Pascal
• Eight Queens program in Java (not on CD, see explanation)

Other Material

• A printer friendly version of all slides
• HTML page for queen program in Java (not available on CD, see explanation)
• A puzzle related to the 8-queens is the knights-tour problem. While slightly more advanced, in Chapter 18 we will introduce the idea of frameworks. In another book I have written an example backtracking framework illustrated using this puzzle.

Intro OOP, Chapter 6, Slide 1

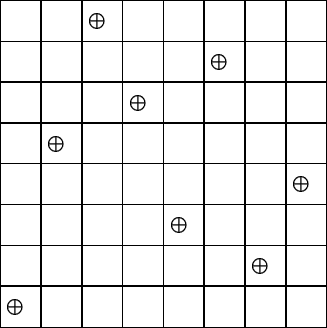
Statement of the Problem

Problem - how to place eight queens on a chessboard so that no two queens can attack each other:

Intro OOP, Chapter 6, Slide 1

OOP Approach

More than just solving the problem, we want to solve the problem in an OOP manner.

• Structure the program so that the data values themselves discover the solution.

• Similar to creating a universe and setting it in motion.

• No single controlling manager.

Intro OOP, Chapter 6, Slide 2

Observations

Here are a few observations we can make concerning this problem:

• Queens can be assigned a column, problem is then to find row positions.

• One obvious behavior is for a queen to tell if it can attack a given position.

• Can structure the problem using generators - each queen can be asked to find one solution, then later be asked to find another solution.

Intro OOP, Chapter 6, Slide 3

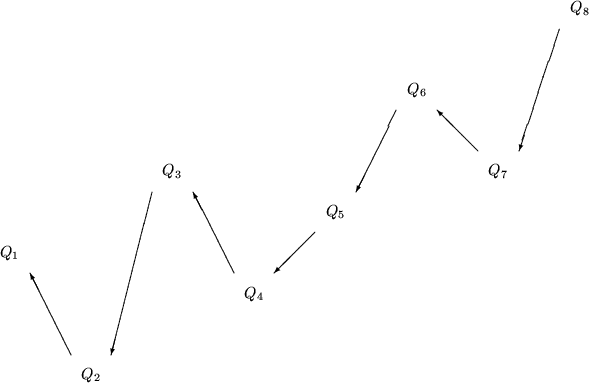
Pointers

We can make each queen point to the next on the left, then send messages only to the rightmost queen. Each queen will in turn send messages only to the neighbor it points to.

Intro OOP, Chapter 6, Slide 4

CRC Card for Queen

Intro OOP, Chapter 6, Slide 5

CRC Card for Queen - Backside

Intro OOP, Chapter 6, Slide 6

Initialization

Initialization will set each queen to point to a neighbor, and set column value. C++ version is shown:

main() {
	Queen * lastQueen = 0;

	for (int i = 1; i <= 8; i++) {
		lastQueen = new Queen(i, lastQueen);
		if (! lastQueen->findSolution())
			cout << "no solution";
	}
	
	if (lastQueen->first()) 
		lastQueen->print();
}

Queen::Queen (int col, Queen * ngh)
{
	column = col;
	neighbor = ngh;
	row = 1;
}

Intro OOP, Chapter 6, Slide 7

Finding First Solution

Finding first solution, in pseudo-code:

function queen.findSolution -> boolean
	
	while neighbor.canAttack (row, column) do
		if not self.advance then
			return false;

		// found a solution
	return true;
end

Intro OOP, Chapter 6, Slide 8

Advancing to Next Position

function queen.advance -> boolean

	if row < 8 then begin
		row := row + 1;
		return self.findSolution
	end

		// cannot go further, move neighbor
	if not neighbor.advance then
		return false

	row := 1
	return self findSolution

end

Intro OOP, Chapter 6, Slide 9

Printing Solution

procedure print
	neighbor.print
	write row, column
end

Intro OOP, Chapter 6, Slide 10

Can Attack

function canAttack(r, c)
	if r = row then
		return true
	cd := column - c;
	if (row + cd = r) or (row - cd = r) then
		return true;
	return neighbor.canAttack(r, c)
end

Intro OOP, Chapter 6, Slide 11

The Last Queen

Two approaches to handling the leftmost queen -

• Null pointers - each queen must then test for null pointers before sending a message

• Special ``sentinel'' value - indicates end of line for queens

Both versions are described in text.

Intro OOP, Chapter 6, Slide 12

Chapter Summary

Important not for the problem being solved, but how it is solved.

• Solution is the result of community of agents working together

• No single controlling program - control is decentralized

• Active objects determine their own actions and behavior.

Intro OOP, Chapter 6, Slide 13