\(\DeclareMathOperator*{\argmax}{\mathrm{argmax}}\)

Knapsack: Unbounded, 0-1, and Bound

Knapsack is a group of classical problems that can be solved by DP.

Three versions of Knapsack: which one is the easiest?

There are three versions of knapsack:

• unbounded knapsack: You take a bag of limited capacity and go to a Costco-like big supermarket where every product has unlimited supply (thus the name “unbounded”). You want to maximize the total value of products that can fit in your bag.
• 0-1 knapsack: This time you go to a very small local convenience store and somehow every product has only one copy (such as one apple, one orange, etc.); basically, for each item, you need to make a binary decision (take it or not), thus the name “0-1”. Equivalently, you need to decide which subset of items to take (as long as they fit in the bag) to maximize the total value of the chosen subset, thus this version is also known as (a general form of) the “subset sum” problem.
• bounded knapsack: This third version is in between unbounded and 0-1, where a smallish store has limited amount of copies for each product (such as three apples and two oranges). Your goal is still to maximize your total value in the bag. This is also the most general case which includes both 0-1 and unbounded as special cases.

Which version is the easiest? Which version is the hardest? Before thinking algorithmically, just think about real-life experience of going shopping.

Well, intuitively, shopping at Costco must be a lot easier than shopping at a local convenience store, because in the former you only need to care about your bag (your only constraint) and not the store (if you like something, you can take as much as you want), whereas in the latter you also need to keep track of the state of the store (“are there still apples left?”), or in other words, you have both the bag capacity constraint and the product availability constraint. Naturally, with more constraints, optimization is harder. Indeed, we will see below that unbounded is much easier to solve algorithmically than 0-1 or bounded.

Between 0-1 and bounded, which one is even harder? Well they are about the same level, because you can convert one to the other and vice versa. If you can solve bounded, then you can obviously solve 0-1 which is a special case; but if you can solve 0-1, you can also use it to solve bounded by converting a bounded problem to a 0-1 one: You can duplicate items in a bounded store, e.g., a “three-apple and two-orange” store can be converted to a 0-1 store with 5 items, [apple1, apple2, apple3, orange1, orange2].

Therefore, unbounded is the easiest, and 0-1 and bounded are about the same level (with the latter just a tiny bit more involved).

Unbounded Knapsack: Costco

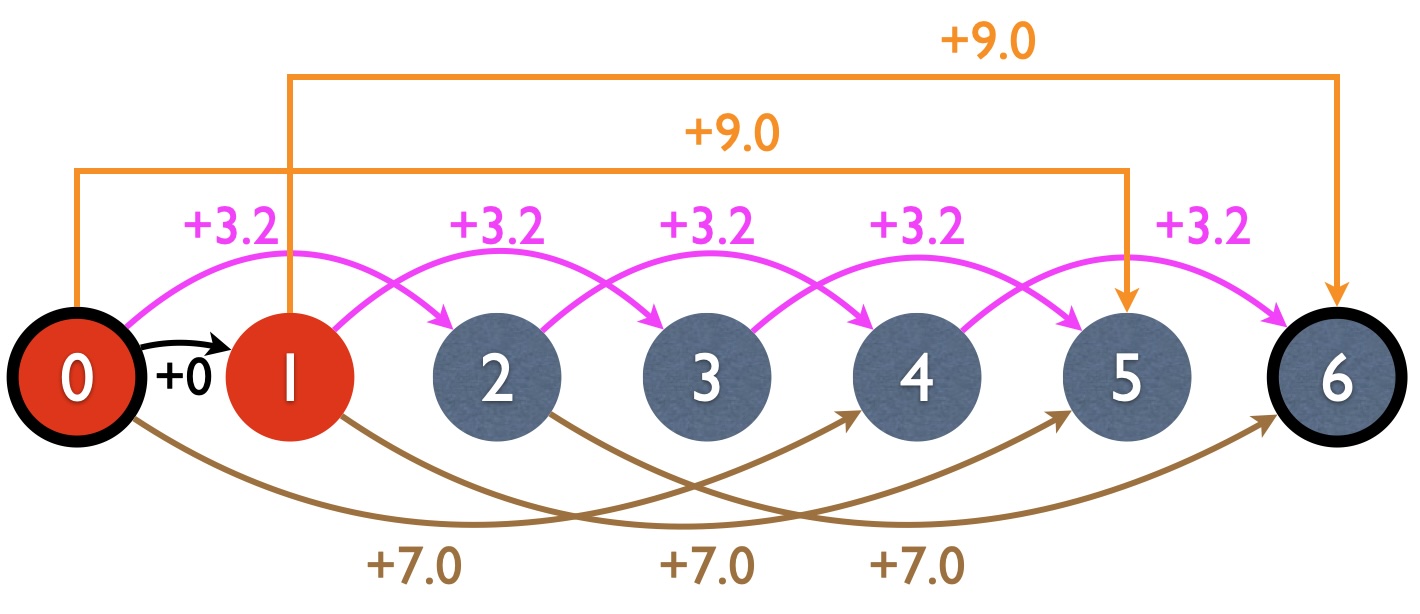
This store has \(n\) products, each with a weight \(w_i\) and value \(v_i\), and each has infinite number of copies. How can you maximaze the total value of products that can fit your shopping bag of capacity \(W\)? You can also view weight \(W\) as your budget and each weight \(w_i\) as the price (which is certainly different from its value to you, \(v_i\); e.g., some products are “overpriced” and of little value or interest to me). For example, \(W=6\), and there are 3 products:

Note that the weights must be integers but values are real numbers.

If we are greedy, we would always pick the product with the highest value (orange) or the highest “value per weight” (still orange), but then our bag can’t fit any other product. So you got a total value of 9.0.

Instead, we can fit three apples in our bag, which gives a total value of 9.6; or even better, we can fit one apple and one pear, which gives a total value of 10.2. So clearly greedy is not optimal.

How would you solve this problem using DP?

Again, think divide-n-conquer: if you can’t solve the problem for a big bag of capacity \(W\), can you solve a similar but smaller subproblem?

So let’s define \(best[w]\) to be the best value for a bag of capacitiy \(w\ (0\leq w \leq W)\). For such a bag \(w\), we can try to put every single product \((w_i, v_i)\) into it and thus shrinking it to an even smaller size \(w-w_i\) but with the reward of \(v_i\), so:

\[ best[w] = \max_{i=1\sim n, w\geq w_i} best[w-w_i] + v_i\]

base case: \(best[0] = 0\); actually not only that, but if a bag is too small for any item, then it must be value 0 as well:

\[ best[w] = 0\quad (0\leq w < \min_i w_i)\]

This simple algorithm has space complexity \(O(W)\) (number of subproblems or table entries) and time complexity \(O(W n)\) (for each subproblem, there is a loop over each \(i\)).

Bottom-Up vs. Top-Down: Which is faster?

Let’s look at the above example for \(W=6\). If you do bottom-up, you would fill each \(best[w]\) for \(w=1,2,3,4,5,6\) (in that order); but you do top-down, you would start with \(w=6\) by calling best(6), and try \(i=1\) first, which calls best(4), which in turn calls best(2), etc. Here is the full recursion tree:

              best(6) = 10.2      -           -                      
        i=1 /           /   |i=2  |     \i=3   \
           /      +v_1 /    |     |+v_2  \      \+v_3
      best(4)= 6.4 -> 7     best(1)=0     best(2)=3.2
  i=1 /   /     \i=3   \
     /   /+v_1   \      \+v_3
best(2)=3.2       best(0)=0
i=1|    |
   |    |+v_1
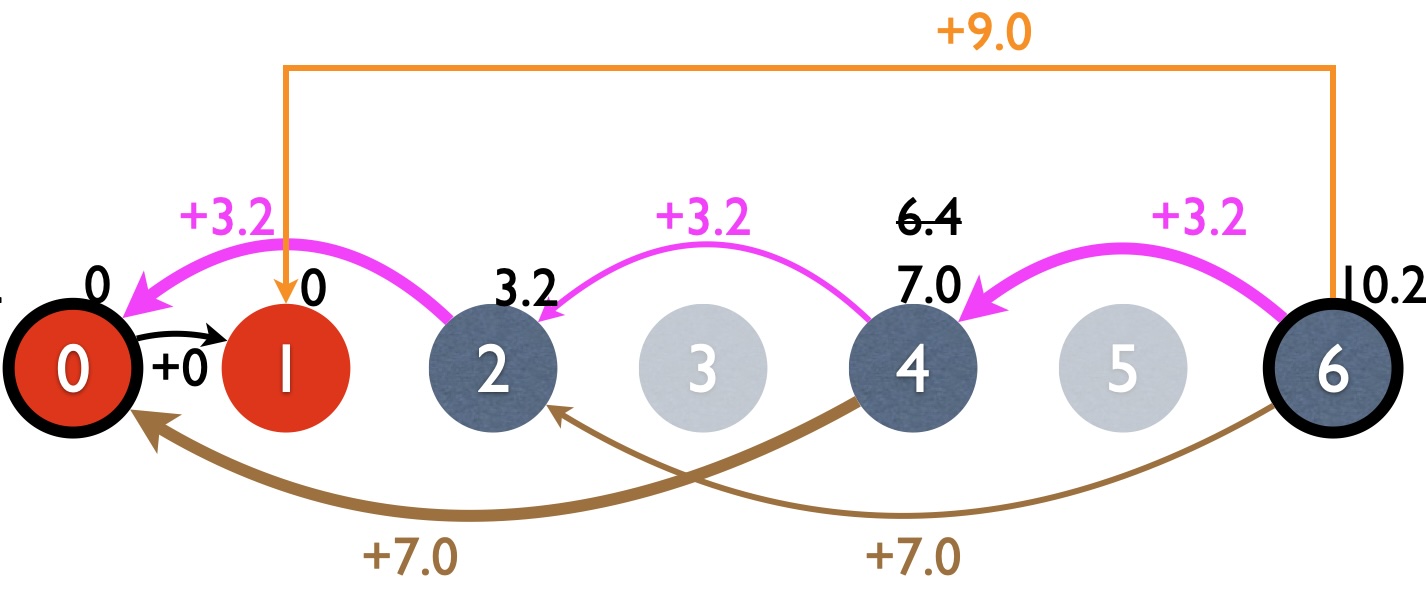
best(0)=0

You notice that best(3) and best(5) are never asked (not to mention solved). Why? Because they are not needed for the global problem best(6), and top-down only asks questions on-demand. If top-down asks best(i), then that subproblem must be potentially useful for the global problem. In this sense you can also view top-down as “lazy”; you’ll find that in computer science, being lazy is one of the highest virtues, and all clever algorithms are lazy.

This example suggests that top-down often solves less subproblems than bottom-up which is “blind” about the future when solving each subproblem one-by-one. To make it more extreme, let’s \(\times 100\) for each \(w_i\) as well as \(W\):

Now bottom-up still needs to solve all 600 subproblems (\(w=1,2,3,4,...,600\)) without knowing the vast majority is not useful. How many would top-down solve? Still just 4 (this time we draw the recursion tree horizontally):

  +------------v
  |            v
600 -> 400 -> 200 -> 0
  |                  ^
  +--> 100 --------->^    

So which order is faster? It depends on the input. If the input is very sparse so that very few subproblems are solved, then top-down is a lot faster; if the input is very dense so that most subproblems are solved, then bottom-up is slightly faster (due to avoiding the overhead for recursion).

Graph Interpretation and Backtracking

As always, each DP problem has a graph interpretation. For MIS, it’s the longest path between source (base case) and target (global subproblem); for Fibonacci or number of bitstrings, it’s the number of paths between source and target.

For unbounded knapsack, like MIS, it’s also the longest path between source and target, the only difference being the graph structure. In MIS, each node (subproblem) has two incoming edges (in graph terminology, we say each node has an in-degree of 2), which correspond to the two choices per node (take or not take \(a_i\)). For unbounded knapsack, however, each node \(best(w)\) has (at most) \(n\) incoming edges, which correspond to each possible product. Here is the DP graph for the running example:

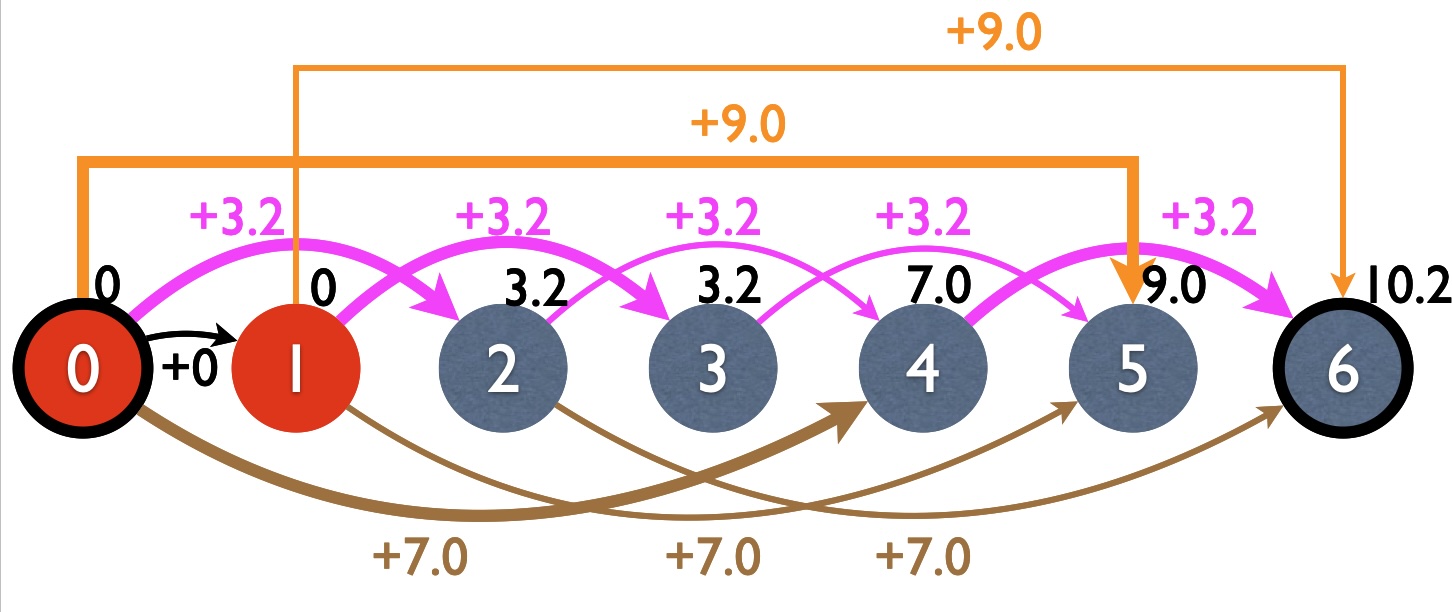
Based on the graph structure, we can figure out the backpointer. In MIS, since each node involves a binary decision, the backpointer for each node is also a boolean. But for our problem, since each node faces a multiple-choice decision, the backpointer will need to remember which item to take (i.e., the best \(i\), or the best incoming edge among all \(n\) of them. Note that in the mathematical notation, the backpointer is always just replacing the \(\max\) in \(best(...)\) with \(\argmax\).

\[ back[w] = \argmax_{i=1\sim n, w\geq w_i} best[w-w_i] + v_i\]

Here is the DP graph after bottom-up, with backpointers in bold edges. Note that each subproblem (i.e., node) is solved, with the best value written in black just above the node.

Finally, here is the DP graph after top-down recursion. Note that some nodes (3 and 5) are never visited because they’re not needed by the global problem. Here I reversed the edge directions to reflect the recursive calls (see recursion trees above). Backpointers are indicated by bold edges.

Space and Time Complexities

In DP, the space complexity is always the number of subproblems (or size of the table for memoization, or number of nodes in the DP graph). So for unbounded, it’s \(O(W)\). The time complexity is basically the space complexity times how many choices you have per subproblem, which is equal to the number of edges in the DP graph. For unbounded, each subproblem faces a multiple choice decision over (at most) \(n\) items and therefore each node has indegree at most \(n\) in the DP graph, so the time complexity is \(O(Wn)\).

0-1 Knapsack (Subset Sum): Local Convenience Store

Now you are back from Costco and enter a local convenience store where each item has only one copy. As discussed above, planning shopping in this setting is much harder than the unbounded case because now you also have the product availability constraint and therefore need to maintain the state of the store (as well as the state of the bag). Naturally, this means your subproblem should not be a one dimensional \(best(w)\), but two dimensional

\[best(w, ???)\]

wotj the “\(???\)” being the “store” dimension. The big question is, what information should we put in that dimension?

Naive Second Dimension: Bit-vector or Subset

A first thought is that we should represent the state of the store by a bit-vector (or boolean array), with each bit corresponding to one product: 1 means that item is still available and 0 means it’s already taken, e.g., 100 means “the apple is still there but the orange and the pear are already taken”. Equivalent, you can have a set \(S\) for the remaining items as the second dimension.

This method is certainly correct, but then this second dimension would have \(2^n\) possibilities (2 choices per item, or the total number of subsets is \(|2^{\{1,...,n\}}|=2^n\)), which means that the new space complexity would be \(O(W \cdot 2^n)\). That’s way too slow due to the exponential growth: \(2^{10} = 1024\), and \(2^{20} \simeq 10^6\). Can we make it faster by avoiding \(2^n\)?

Smart Second Dimension: Shrink the Store

For the second dimension, think about the MIS problem in Sec. 2.1, which is also a subset optimization problem (with the additional constraint of “independent subset”). In total, there are also \(O(2^n)\) possibilities, but you can solve it in \(O(n)\) time by considering “take” or “not take” for each item \(i\) sequentially. Each time you shrink the problem by one (or two) item(s).

Same idea here. You enter a 0-1 store and you say to the owner “your store is too big for me to solve and I’m going to divide-n-conquer and I’ll shrink your store by one item”. Basically you have two possible actions:

• take item \(i\), then the store shrinks by 1 to \(i-1\), and your bag also shrinks by \(w_i\);
• don’t take item \(i\), then only the store shrinks to \(i-1\) but your bag stays the same.

This is somewhat similar to but also different from MIS where the cost of taking item \(i\) is that you have to skip item \(i-1\).