Parameterization definition. A curve (or surface) is parameterized if there's a mapping from a line (or plane) to the curve (or surface). So, for example, you might parameterize a line by:
l(t) = p + tv, p a point, v a vector.
The mapping is a function that takes t to a curve in 2D or 3D. For surfaces, the mapping is a function that takes two parameters (s,t) to a surface in 3D. (Actually parameterization works for any input dimension, and any output dimension, but the most common mappings in graphics are the three listed above.)
Why parameterize? There's a lot of reasons.
Some definitions of terms that show up in parameterization papers.
The goal of this work is to introduce manifolds as a technique for representing parameterizations. There are many surface representations that do not have a natural parameterization; two common examples are meshes and implicit surfaces. There are several techniques for parameterizing meshes (see below), which range from ad-hoc to fairly well principled. Most of these techniques are complementary to the problem proposed here.
It's fairly well understood how to do parameterization from a plane to a surface. The problem with these parameterizations is that they're limited to shapes that have the topology of a plane - think of a bendy, stretchy piece of rubber. There is no way to do a single, global, smooth parameterization of a spherical object, or objects with multiple handles or holes. The standard thing to do in this case is take individual, planar parameterizations and "glue" them together at the edges geometrically, creating a patchwork effect.
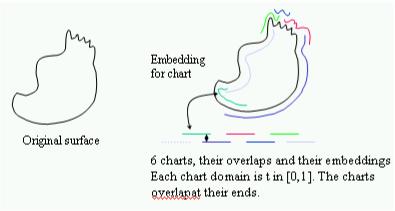
Manifolds are a technique for building arbitrary topology parameterizations that are smooth - they're just not global. Instead of gluing individual parameterizations together at the edges, manifolds glue them by overlapping the parameterizations. Think of a world atlas - each page is a local parameterization of some part of the world. Together, they cover the entire world. The pages overlap at the boundaries - they may not line up perfectly, but it's easy to navigate from one page to another.

Most parameterization techniques work by cutting up arbitrary topology surfaces into smaller pieces that can be parameterized with one or more planes. This introduces seams into the parameterization. It's possible to work around the seams by placing them where they're inconspicuous, or by writing code that specifically deals with the problem.
Manifolds provide a "nice" way of handling these boundaries. The individual parameterizations can be defined so they overlap a fair amount, which provides lots of room to transition from one parameterization to another. Since the parameterizations overlap there are no seams, just transition regions and equations for mapping from one parameterization to the next. They also have a built-in method for "blending" functions across parameterizations.
Most parameterization techniques focus on how to "flatten out" the surface into the plane while maintaining some properties as best as possible (such as area). These techniques are used to produce the mapping between the manifold and the surface.
The approach taken in this work is to produce a C^infinity manifold for each genus type (sphere, plane, n-holed torus, etc.). The manifolds have several desirable properties, such as unit square domains, substantial overlap, and a small number of parameterizations or charts.
Given a surface, we use the manifold with the same topology for the parameterization. The bulk of the work is in establishing a 1-1, onto correspondence between the surface and the manifold. This mapping is not necessarily smooth, since the original surface might not be (meshes, for example).
We can introduce geometry to the manifold by embedding it. We've experimented with spline and radial basis function embeddings. Using this embedding, we can produce a smooth approximation or interpolation of our input surface. Since the manifold embedding is analytical, we can calculate derivatives, curvature, etc.
Manifolds. Siggraph '95. I've included this paper because it has a good description of manifolds and how to construct one versus using manifolds to analyze an existing surface (the usual use of manifolds). The manifold construction itself is a bit cumbersome and expensive. It starts with a mesh and builds a parameterization for each element (vertex, edge, and face). Don't even bother looking at the embedding equations (horribly complex), although the method for blending functions on charts is the one we currently use.