Improved OT Extension for Transferring Short Secrets

Improved OT Extension for Transferring Short Secrets

Vladimir Kolesnikov, Ranjit Kumaresan
CRYPTO 2013 [pdf] [bibtex]

Prerequisite:

This summary expects the reader to have a basic understanding of the IKNP03 protocol.

Introduction

KK describe an generalization and optimization to IKNP03 protocol for ⚠️{$OT$} extension in the semi-honest setting. The protocol provides a ⚠️{$O(\log k)$} performance improvement over the IKNP 1-out-of-2 ⚠️{$OT$} protocol and generalizes it to a 1-out-of-⚠️{$n$} ⚠️{$OT$} with the same asymptotic improvement over the state of the art 1-out-of-⚠️{$n$} ⚠️{$OT$}. The protocol is also applicable in the multi-party setting unlike the original IKNP version. In concrete terms, this yields a 2-3 factor performance improvement for the 1-out-of-2 ⚠️{$OT$} protocol.

The main observation made by KK is that in the IKNP protocol, the ⚠️{$Receiver$}'s selection vector ⚠️{$r$} is reused on each of the ⚠️{$k$} initial ⚠️{$OT$}s. This can be seen below on the left.

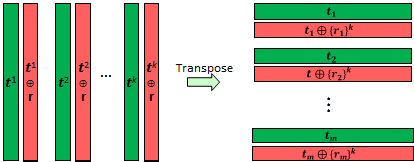
On each one of the (red/green) Column pairs, a 1-out-of-2 ⚠️{$OT$} is performed in the IKNP protocol. If you take the transpose of these columns, each red row encoding is ⚠️{$t_j\oplus \{1\}^k$} or ⚠️{$t_j\oplus \{0\}^k$} based upon the bit ⚠️{$r_j$}. Inspired by the observation that these repetitious codes (⚠️{$\{1\}^k$} and ⚠️{$\{0\}^k$}) dictate the receivers selection, what if the codes were vectors of ⚠️{$\{0,1\}^k$}. Would this enable to protocol to generalize to a 1-out-of-⚠️{$n$} ⚠️{$OT$}?

To accommodate a 1-out-of-⚠️{$n$} ⚠️{$OT$} protocol, the IKNP ⚠️{$Receiver$} selection vector ⚠️{$r\in \{0,1\}^m$} will need to be expanded to ⚠️{$r\in \{0,1,...,n-1\}^m$} to denote the ⚠️{$Receiver$}'s 1-out-of-⚠️{$n$} selection on all ⚠️{$m$} ⚠️{$OT$}s.

To securely achieve this result, the new ⚠️{$\{0,1\}^k$} vector codes will need to have a relative distance of ⚠️{$\frac{1}{2}$} between each other. That is, each code must be different enough from the others to maintain the security. The Walsh-Hadamard codes have this exact property. We will denote the Walsh-Hadamard encoding of ⚠️{$r_j$} as ⚠️{$c(r_j)$}.

1-out-of-n Protocol

Let the ⚠️{$Receiver$} generate ⚠️{$T_0$} as a ⚠️{$m \times k$} random bit matrix, shown below as the green vectors. Let ⚠️{$T_1$} be the matrix whose ⚠️{$j^{th}$} row is the ⚠️{$j^{th}$} row of ⚠️{$T_0$} XOR ⚠️{$c(r_j)$}, as seen below by the red vectors. Note: ⚠️{$k$} is the security parameter.

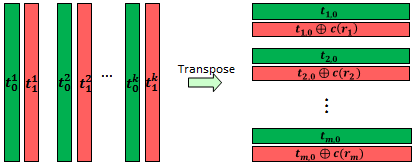
where ⚠️{$t_{j,0}$} is the ⚠️{$j^{th}$} row of ⚠️{$T_0$}, and ⚠️{$t_x^i$} is the ⚠️{$i^{th}$} column of ⚠️{$T_x$}

The protocol now performs ⚠️{$k$} 1-out-of-2 ⚠️{$OT$}s on the ⚠️{$k$} columns of the two matrices ⚠️{$T_0$} and ⚠️{$T_1$}, where the ⚠️{$Receiver$} acts as the sender. Note: these ⚠️{$OT$}s are the same as the IKNP protocol except that the rows of ⚠️{$T_1$} are ⚠️{$t_{j,0}$}⚠️{$\oplus c(r_j)$} instead of ⚠️{$t_{j,0}$}⚠️{$\oplus \{r_j\}^k$}.

As before in IKNP, the ⚠️{$Sender$} will randomly select between these two (red/green) columns for each of the ⚠️{$k$} pairs. Let ⚠️{$s\in \{0,1\}^k$} be the vector denoting this random selection and let ⚠️{$Q$} be the matrix denoting the collection of these ⚠️{$k$} ⚠️{$OT$}s when they are stored column wise. That is ⚠️{$q^i=t^i_{s_i}$}

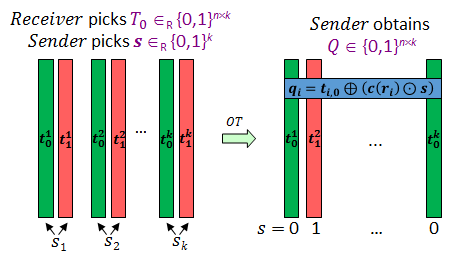
As shown in blue, each row of ⚠️{$Q$} (denoted as ⚠️{$q_i$}) will be the corresponding row in ⚠️{$T_0$} XORed with the Walsh-Hadamard code for ⚠️{$r_i$} bitwise ANDed with ⚠️{$s$}. The main take away here is that each row of ⚠️{$Q$} has 1-out-of-⚠️{$n$} possible values if you fix ⚠️{$T_0$} and ⚠️{$s$}. In particular, this 1-out-of-⚠️{$n$} decision is made by the ⚠️{$Receiver$} and is unknown to the ⚠️{$Sender$}.

The initialization phase has now completed and the real 1-out-of-⚠️{$n$} ⚠️{$OT$}s can now be performed.

The ⚠️{$Sender$} will send the ⚠️{$Receiver$} an one time pad encryption of each of the ⚠️{$n$} messages for each of the 1-out-of-⚠️{$n$} ⚠️{$OT$}s. The ⚠️{$i^{th}$} messages in this ⚠️{$OT$} will be encrypted with the hash, ⚠️{$H(j,q_j\oplus ( c(i)\odot s ))$} as a one time pad mask. Based upon the ⚠️{$receiver$}'s choice of ⚠️{$r_j$}, exactly one of these messages will be equivalent to ⚠️{$H(j,$}⚠️{$t_{j,0}$}⚠️{$)$}. That is ⚠️{$q_j\equiv $}⚠️{$t_{j,0}$}⚠️{$\oplus (c(r_j)\odot s)$} will cancel with ⚠️{$( c(i)\odot s )$} leaving ⚠️{$t_{j,0}$} when ⚠️{$i=r_j$}.

Put algorithmically,
For each ⚠️{$j$} in the ⚠️{$m$} ⚠️{$OT$}s:

For each ⚠️{$i$} in the ⚠️{$n$} messages of the ⚠️{$j^{th}$} ⚠️{$OT$}:
The ⚠️{$Sender$} sends the ⚠️{$Receiver$}: ⚠️{$y_{j,i}=M_{j,i}\oplus H(j,q_j\oplus ( c(i)\odot s ))$}

Where ⚠️{$M_{j,i}$} is the ⚠️{$i^{th}$} message of the ⚠️{$j^{th}$} ⚠️{$OT$}.

The ⚠️{$Receiver$} will then decrypt the ⚠️{$y_{j,r_j}$} message by re-XORing ⚠️{$y_{j,r_j}$} with ⚠️{$H(j,$}⚠️{$t_{j,0}$}⚠️{$)$}. This results in ⚠️{$M_{j,r_j}$}, which is precisely the ⚠️{$Receiver$}'s desired message on the ⚠️{$j^{th}$} ⚠️{$OT$}. All of the other message encryptions of the ⚠️{$j^{th}$} ⚠️{$OT$} will remain pseudo random because the ⚠️{$Receiver$} does not know the random bit vector ⚠️{$s$} that the ⚠️{$Sender$} picked.

In sum, ⚠️{$m$} instances of a 1-out-of-⚠️{$n$} ⚠️{$OT$} can be obtained by ⚠️{$k$} instances of a 1-out-of-2 ⚠️{$OT$} plus at most ⚠️{$mn$} calls to a random oracle by both parties. Since ⚠️{$k$} is the security parameter this can yeild a significant improvement when ⚠️{$m$} becomes large.

1-out-of-2 Optimization

Let ⚠️{$n\choose 1$}-⚠️{$OT_{l}^{m}$} denote ⚠️{$m$} instances of a 1-out-of-⚠️{$n$} ⚠️{$OT$} each of length ⚠️{$l$}.

From an observation not shown here, ⚠️{$\log n$} instances of a ⚠️{$2\choose 1$}-⚠️{$OT$} can be obtained from a single instance of ⚠️{$n\choose 1$}-⚠️{$OT$} of slightly longer message length. Put precisely, a ⚠️{$2\choose1$}-⚠️{$OT_{l}^m$} has the same exact cost as a ⚠️{$n\choose 1$}-⚠️{$OT_{l\log n}^{m/\log n}$}. This hints that the generalization KK describe can also be used to further optimize the 1-out-of-2 variant.

With the use of this observation, ⚠️{$m$} instances of a 1-out-of-2 ⚠️{$OT$} can be obtained with the additional asymptotic cost of ⚠️{$O(mk/\log(k/l))$}, where ⚠️{$k$} is the security parameter. This contrasts with the IKNP cost of ⚠️{$O(m(k+l))$}. In the important case when ⚠️{$l=1$}, we obtain a logarithmic improvement over IKNP.

Random Oracle

Similar to the IKNP protocol, a ⚠️{$Code$}-⚠️{$Correlation$} ⚠️{$Robust$} random oracle is required to ensure a semi-honest ⚠️{$Receiver$} cannot learn ⚠️{$s$} and therefore all of ⚠️{$M$}. ⚠️{$Code$}-⚠️{$Correlation$} ⚠️{$Robustness$} is a property of a random oracle ensuring that no information about the input is leaked when the input are known values XORed/ANDed with an unknown value. Even if polynomial many queries with different know values are made. Specifically, the joint distribution of

⚠️{$\{t_1,t_2,...,t_n\}$} , ⚠️{$\{c_1,c_2,...,c_n\}$} and ⚠️{$H(t_j\oplus (c_{j'}\odot s)),H(t_l\oplus (c_{l'}\odot s)),...,H(t_n\oplus (c_{n'}\odot s)) $}

must be pseudo random, where ⚠️{$s$} is unknown and ⚠️{$H$} is queried a polynomial number of times with respect to the security parameter. This is a requirement because the ⚠️{$Receiver$} knows all of these ⚠️{$t_i$} and ⚠️{$c_i$} values. i.e. ⚠️{$t_{i,0}$} and ⚠️{$c(r_i)$}. If the correlations between the inputs and the hash values are not pseudo random, the ⚠️{$Receiver$} could learn ⚠️{$s$}, and thereby all of ⚠️{$M$}.

Summary

In summary, this protocol reduces ⚠️{$m$} instances of a 1-out-of-⚠️{$n$} ⚠️{$OT$} to a small security parameter number of 1-out-of-2 ⚠️{$OT$}s. In practice ⚠️{$m$} can be several orders of magnitude larger than the security parameter ⚠️{$k$}. For example ⚠️{$m=30000, k=256$}. This yields a significant performance increase over a nave implementation of ⚠️{$m$} instances of a 1-out-of-⚠️{$n$} ⚠️{$OT$}. At the time this paper was published, the protocol results in a logarithmic improvement over the state of the art, which translates to an approximate speed up of 5 fold.

In addition, this 1-out-of-⚠️{$n$} protocol yields a performance improvement for the 1-out-of-2 variant when they are implemented by a black box use of this 1-out-of-⚠️{$n$} protocol. Beyond these improvement, KK describe another optimization by using a pseudo random generator instead of the completely random matrix ⚠️{$T_0$}.

References:

IKNP03

Other links:

CRYPTO presentation video

Categories:

OTExtension Todo