A Hybrid Lagrangian-Eulerian (hLE) Scheme for Interface Tracking

Development of numerical methods to accurately track/capture the interface between two fluids has been an area of research for decades. Tryggvason et al. (JCP 2001) provide a detailed review on various numerical approaches. Broadly, these schemes can be classified into two categories: front tracking and front capturing methods. In the present work, some of the limitations of the above schemes are addressed by combining these two approaches. The basic idea is to merge the locally `adaptive' mesh-free particle-based methods with the relative `ease' of Eulerian finite-volume formulation in order to inherit the advantages offered by individual approaches. Our main motivation for this approach stems from the fact that most research codes or commercial softwares modeling particle-laden or bubbly flows, spray dynamics etc. have routines for tracking of Lagrangian marker points. The idea is to build modules that will make use of this point-particle tracking infrastructure and apply them, with relative ease, to simulate fully resolved deforming interfaces. The approach developed here is modular and thus can be easily incorporated (in theory!) into any research solver or commercial software.

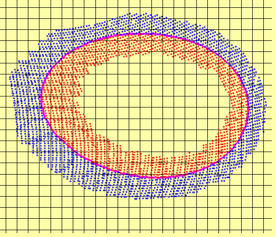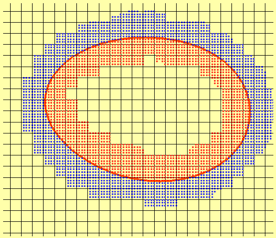
Lagrangian Points (LPs) representing an interface: (left) distorted LPs, (right) reconfigured LPs.

In this approach, the interface between the two fluids is represented and tracked using Lagrangian points (LPs) or fictitious particles (Hieber and Koumoutsakos, JCP 2005). Unlike particle level set (Enright et al., JCP 2002) or the semi-Lagrangian methods (Strain, JCP 2001), in the present approach the interface is represented by LPs that are advanced in a Lagrangian frame. The motion of the interface is determined by a velocity field (interpolated to the particle locations) obtained by solving the Navier-Stokes equations on a fixed background mesh in an Eulerian frame. The potential advantage of the present hybrid method is that the background mesh could be of any kind: structured or arbitrary shaped unstructured (hex, pyramids, tetrahedrons, prisms) and may be stationary or changing in time (adaptive refinement). Although the interface is represented by LPs, this approach does not require connectivity information among the LPs, thus avoiding complex triangulation or reconstruction algorithms for the interfacial surface. Our approach has characteristics of the point-set method (Torres and Brackbill, JCP 2000); however, does not require solution of a Laplace equation for estimating color function. This approach has been developed and a series of fundamental test cases have been performed to evaluate its accuracy in comparison to other existing schemes showing promising results.

We presently are working on domain-decomposition strategies for efficient parallelization of the hLE approach.

• Apte, S.V., Shams, E., and Finn, J., A hybrid Lagrangian-Eulerian approach for simulation of bubble dynamics, Seventh International Symposium on Cavitation, University of Michigan, Ann Arbor, 2009. (PDF)

• Apte, S.V., A hybrid Lagrangian-Eulerian method for interface tracking, ILASS Americas 21st Annual Conference on Liquid Atomization and Spray Systems, Orlando, FL, May 2008. (PDF)

• Shams, E., and Apte S.V., A hybrid Lagrangian-Eulerian (hLE) scheme for simulations of dispersed two-phase flows with fully resolved interfaces, ILASS America's 20th Annual Conference on Liquid Atomization and Spray Systems, Chicago, IL, May 2007. (PDF)