A Numerical Scheme for Moving Boundary Problems

Flow over arbitrary shaped rigid moving boundaries are common in many practical systems. These flows can be categorized by the type of the rigid boundary motion: (i) flow past a rigid boundary with specified boundarymotion, and (ii) flow past freely moving suspended rigid objects with fluid-particle interactions.

Several numerical approaches such as Immersed Boundary Method (IBM), Lattice Boltzmann Method (LBM), Distributed Lagrange Multiplier (DLM) based Fictitious Domain Methods, Arbitrary Lagrangian Eulerian (ALE), Boundary Element Method, and several combinations of these approaches have been developed for these problems.

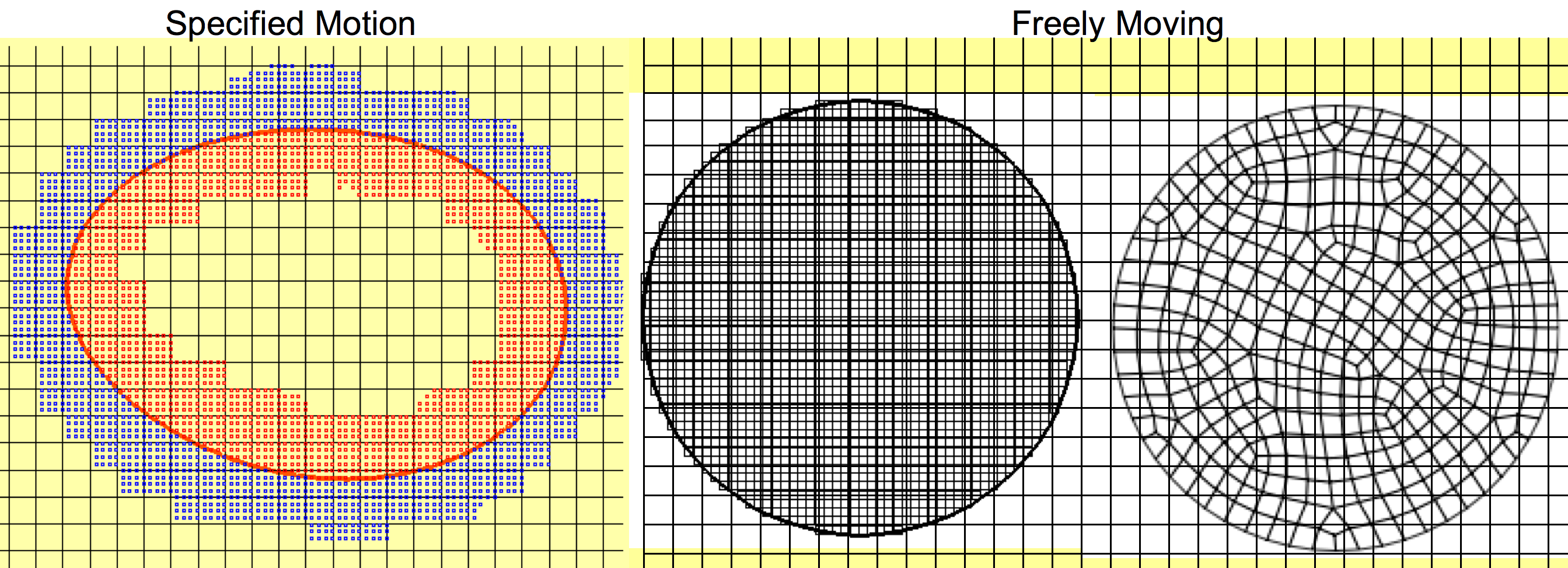
We are developing a Fictitious-Domain based second-order scheme for turbulent flow simulations. In this approach, the entire fluid-rigid body domain is assumed to be an incompressible, but variable density, fluid. The flow inside the fluid region is constrained to be divergence-free for an incompressible fluid, whereas the flow inside the particle (or rigid body) domain is constrained to undergo rigid body motion. For specified motion of the rigid body, the rigidity constraint can be readily obtained once the location of the boundary of the rigid body is identified (for example, flow over a cylinder at Re=1000 as shown above). For these problems, we use marker points in a banded region surrounding the rigid body surface similar to the hybrid Lagrangian-Eulerian (hLE) scheme. Due to rigidity of the moving object, there is no relative motion between the marker points, and all points move with the same, specified velocity field. The rigidity constaint is then enforced explicitly in a standard fractional step scheme. This approach can also be applied to motion of flexible bodies when the boundary deformation is known (for example, specified undulatory motion of an eel).

For the second class of problems, the rigid body is freely suspended in a fluid and undergoes free rotation and translation. The rigid body velocity is unknown. We obtain this velocity field in the context of a three-stage fractional step scheme. Once the rigid body motion is computed, the rigidity constraint force can be readily obtained and imposed for the fictitious fluid within the rigid body region. For these problems, we define the shape of the rigid body by creating small material points within the rigid body. We have implemented this approach in a structured, co-located grid fractional step scheme suitable for fully resolved direct simulations of particle-laden turbulent flows.

Typically, this approach together with several other numerical schemes for freely moving rigid particles provide stable solutions for fluid-particle systems at low density ratios (on the order of 10) between the fluid and the particle. We are presently developing a variable-density fictitious domain method for high-density ratio (on the order of 1000 and more) for practical fluid-particle systems such as coal reactors, fluidized beds, aeolion transport, among others.

• Apte, S.V., and Finn, J., A variable density fictitious domain method for fully resolved simulation of high-density ratio fluid-particle systems, ICMF2010, Seventh International Conference on Multiphase Flow, Tampa Bay, FL, 2010. (PDF)

• Apte S.V., Martin, M., and Patankar, N.A., 2008, A numerical method for fully resolved simulation (FRS) of rigid particle-flow interactions in complex flows, Journal of Computational Physics, accepted for publication. (PDF)

• Apte S.V., and Patankar N.A., 2008, A formulation for fully resolved simulation (FRS) of particle-turbulence interactions in two-phase flows, International Journal of Numerical Analysis and Modeling, Vol. 5, Suppl., pp. 1-16. A special issue on Modeling, Analysis, and Simulations of Multiscale Nonlinear Systems. (PDF)

• Mathieu, M., Patton, C., Schmitt, J., and Apte S.V., 2009, Direct simulation based model-predictive control of flow maldistribution in parallel microchannels, Journal of Fluids Engineering, Vol. 131 (11), pp. 111201-111218. (PDF)